题目内容
【题目】已知椭圆![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,
,![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() .
.
(1)求![]() 的方程;
的方程;
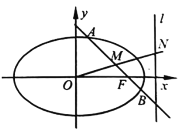
(2)若点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() ∥
∥![]() .判断
.判断![]() 是否为定值,若是求出该值;若不是请说明理由.
是否为定值,若是求出该值;若不是请说明理由.
【答案】(1)![]() (2)是定值,
(2)是定值,![]() 为定值2.
为定值2.
【解析】
(1)先求出抛物线![]() 的焦点
的焦点![]() 的坐标,再由
的坐标,再由![]() 经过点
经过点![]() 得出
得出![]() 的值,最后利用椭圆的定义以及题中条件求出
的值,最后利用椭圆的定义以及题中条件求出![]() ,从而得解;
,从而得解;
(2)先设出直线![]() 的方程,求出点
的方程,求出点![]() 的坐标,可得
的坐标,可得![]() 的值,再把
的值,再把![]() 的方程与
的方程与![]() 的方程联立,求出点
的方程联立,求出点![]() 的坐标,从而得
的坐标,从而得![]() 的值,根据已知求出
的值,根据已知求出![]() ,根据椭圆的对称性,求出
,根据椭圆的对称性,求出![]() ,即可判断
,即可判断![]() 是否为定值.
是否为定值.
(1)因为抛物线![]() 的焦点
的焦点![]() ,所以
,所以![]() ,
,
因为![]() 上的点
上的点![]() 与
与![]() 的两个焦点所构成的三角形的周长为
的两个焦点所构成的三角形的周长为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的方程为
的方程为![]() .
.
(2)由题意可知直线![]() 的斜率存在且不为0,设直线
的斜率存在且不为0,设直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
由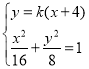 ,得
,得![]() ,解得
,解得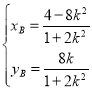 ,
,
即 , 所以
, 所以![]() ,
,
因为![]() ∥
∥![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
由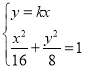 ,得
,得![]() ,解得
,解得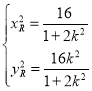 ,
,
所以![]() ,
,
根据椭圆的对称性,知![]() ,即
,即![]() ,
,
所以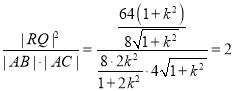 ,
,
故![]() 为定值,该定值为2.
为定值,该定值为2.

【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: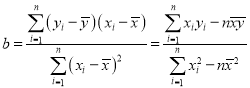 ,
,![]() .
.
【题目】某种治疗新型冠状病毒感染肺炎的复方中药产品的质量以其质量指标值衡量,质量指标越大表明质量越好,为了提高产品质量,我国医疗科研专家攻坚克难,新研发出![]() 、
、![]() 两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于
两种新配方,在两种新配方生产的产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于![]() 时为废品,指标值在
时为废品,指标值在![]() 为一等品,大于
为一等品,大于![]() 为特等品.现把测量数据整理如下,其中
为特等品.现把测量数据整理如下,其中![]() 配方废品有
配方废品有![]() 件.
件.
![]() 配方的频数分布表
配方的频数分布表
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)求![]() ,
,![]() 的值;
的值;
(2)试确定![]() 配方和
配方和![]() 配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)
配方哪一种好?(说明:在统计方法中,同一组数据常用该组区间的中点值作为代表)