Question

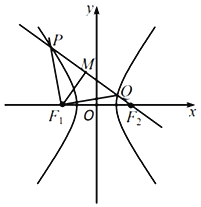
【题目】已知抛物线的焦点为，准线与轴交于点，过点的直线交抛物线于，两点，点在第一象限.

若，，求直线的方程；

若，点为准线上任意一点，求证：直线，，的斜率成等差数列.

Answer 1

【答案】；证明见解析.

【解析】

设点在准线上的射影为，由抛物线的定义知，，设，列式联立求出，直线AB的斜率为，进而写出直线的方程；

若，则抛物线，准线，设直线的方程为，

联立得消得，利用韦达定理，进而求出，即可求证.

解：设点在准线上的射影为，由抛物线的定义知，

，设，，由题设知，

，，

解得，则，，即，①

又由抛物线的定义知，，即，②

联立①②，解得，或，

，∴，则，

焦点为，，

则直线的斜率为，

故直线的方程为；

证明：若，则抛物线，

，准线，

设直线的方程为，

，，，

由消去得，，

则，，

则

又，，

故直线，，的斜率成等差数列.