题目内容
【题目】如图,在正四棱柱![]() 中,
中,![]() ,
,![]() ,点E在
,点E在![]() 上,且
上,且![]() .
.
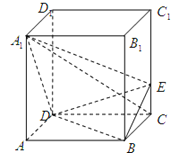
(1)求异面直线![]() 与
与![]() 所成角的正切值:
所成角的正切值:
(2)求证:![]() 平面DBE;
平面DBE;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据![]() 可知
可知![]() 即为所求异面直线所成角,根据直角三角形中的长度关系可求得结果;
即为所求异面直线所成角,根据直角三角形中的长度关系可求得结果;
(2)以![]() 为原点建立空间直角坐标系,根据数量积的坐标运算可证得
为原点建立空间直角坐标系,根据数量积的坐标运算可证得![]() ,
,![]() ,由线面垂直判定定理可证得结论;
,由线面垂直判定定理可证得结论;
(3)由(2)知![]() 为平面
为平面![]() 的一个法向量,求得平面
的一个法向量,求得平面![]() 的法向量
的法向量![]() 后,可根据向量夹角公式求得
后,可根据向量夹角公式求得![]() ,由二面角的大小可确定最终的余弦值.
,由二面角的大小可确定最终的余弦值.
(1)![]()
![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角
所成角
在![]() 中,
中,![]() ,
,![]()
![]()
即异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]()
(2)以![]() 为原点,可建立如下图所示的空间直角坐标系
为原点,可建立如下图所示的空间直角坐标系

则,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
又![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
(3)由(2)知:向量![]() 为平面
为平面![]() 的一个法向量
的一个法向量
设平面![]() 的法向量
的法向量![]()
则 ,令
,令![]() ,则
,则![]() ,
,![]()
![]()
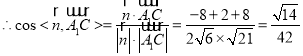
![]() 二面角
二面角![]() 为锐二面角
为锐二面角 ![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]()

【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()