题目内容
【题目】如图，
垂直于以
为直径的圆所在的平面，点
是圆周上异于
，
的任意一点，则下列结论中正确的是（ ）
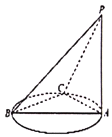
①
②
③
平面
④平面
平面
⑤平面
平面
A.①②⑤B.②⑤C.②④⑤D.②③④⑤
【答案】B
【解析】
①假设
，可证
面
，推出
，矛盾.
②由
，
，得
平面
即可.
③假设平面，推出，矛盾.
④假设平面
平面，由②知平面
平面，推出
平面，矛盾.
⑤论证平面，再用面面垂直的判定定理判断.
①若，因为
平面
,所以
，又因为
,所以面，又因为
面，所以，故错误.
②因为平面,所以，又因为，
，所以平面,所以
，故正确.
③若平面，则，显然错误.
④若平面平面 ，由②知平面，又
平面，所以平面平面，所以平面（因为若两个平面同垂直于另一个平面，则它们的交线也垂直于这个平面），故错误.
⑤由②知平面，又平面，所以平面平面，正确.
故选：B
练习册系列答案
相关题目
