题目内容
16.已知数列{an}是各项均不为0的等差数列,Sn为其前n项和,且对任意正整数n都有an2=S2n-1.(1)求数列{an}的通项公式;
(2)若数列$\{\frac{b_n}{{{a_{n-1}}}}\}$是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.
分析 (1)设等差数列{an}的公差为d,an≠0.对任意正整数n都有an2=S2n-1,可得${a}_{1}^{2}$=a1,${a}_{2}^{2}=({a}_{1}+d)^{2}$=S3=$3{a}_{1}+\frac{3×2}{2}d$,解得a1,d,即可得出.
(2)$\frac{{b}_{n}}{{a}_{n-1}}$=•3n-1,可得bn=(2n-3)•3n-1,利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,an≠0.
对任意正整数n都有an2=S2n-1,∴${a}_{1}^{2}$=a1,${a}_{2}^{2}=({a}_{1}+d)^{2}$=S3=$3{a}_{1}+\frac{3×2}{2}d$,
解得a1=1,d=2,或-1(舍去).
∴an=1+2(n-1)=2n-1.
(2)$\frac{{b}_{n}}{{a}_{n-1}}$=•3n-1,∴bn=(2n-3)•3n-1,
∴数列{bn}的前n项和Tn=-1+3+3×32+…+(2n-3)•3n-1,
∴3Tn=-3+32+3×33+…+(2n-5)•3n-1+(2n-3)•3n,
∴-2Tn=-1+2(3+32+…+3n-1)+(2n-3)•3n=-1+2×$\frac{3({3}^{n-1}-1)}{3-1}$-(2n-3)•3n,
∴Tn=2+(n-2)•3n.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知△OAB的直观图△O′A′B′(如图)O′A′=1,∠B′=30°,则△OAB的面积为( )
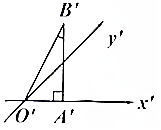

| A. | $\sqrt{6}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\sqrt{3}$ |
11.已知非零常数α是函数y=x+tanx的一个零点,则(α2+1)(1+cos2α)的值为( )
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
1.已知复数$\frac{2+i}{a-i}$(其中a∈R,i为虚数单位)是纯虚数,则a+i的模为( )
| A. | $\frac{5}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{5}$ |
5.设i为虚数单位,复数$\frac{a+2i}{1+i}$为纯虚数,则实数a的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |