题目内容
10．某几何体的三视图如图所示，其中俯视图为扇形，则该几何体的体积为（ ）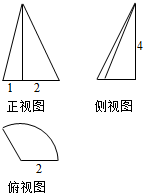
| A． | $\frac{2π}{3}$ | B． | $\frac{16π}{9}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{9}$ |
分析 几何体为圆锥的一部分，求出几何体底面扇形的圆心角即可得出几何体与圆锥的体积比．
解答 解：由三视图可知几何体为圆锥的一部分，圆锥的底面半径为2，高为4，∴圆锥的体积V圆锥=$\frac{1}{3}×π×{2}^{2}×4$=$\frac{16π}{3}$．
几何体的底面扇形圆心角为π-arccos$\frac{1}{2}$=$\frac{2π}{3}$．
∴几何体体积V=$\frac{\frac{2π}{3}}{2π}$•V圆锥=$\frac{16π}{9}$．
故选B．
点评 本题考查了圆锥的三视图与结构特征，属于基础题．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
20．某几何体的三视图如图所示，在该几何体的各个面中，面积最小的面与底面的面积之比为（ ）
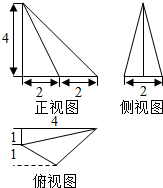
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{4}{5}$ |
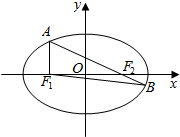如图，点F1，F2分别是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点．点A是椭圆C上一点，点B是直线AF2与椭圆C的另一交点，且满足AF1⊥x轴，∠AF2F1=30°．
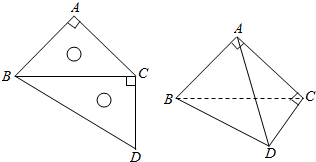一副三角板如图拼成，AB=AC，∠BAC=90°，∠DBC=30°，∠BCD=90°，将△BCD沿BC折起，使得平面ABC⊥平面BCD．
在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别为A1D1和A1B1的中点．
20．抛物线y=$\frac{1}{2}$x2的焦点坐标是（ ）
| A． | （0，$\frac{1}{8}$） | B． | （-$\frac{1}{8}$，0） | C． | （-$\frac{1}{2}$，0） | D． | （0，$\frac{1}{2}$） |