题目内容
7.给出以下结论:①函数$y=\frac{1}{x}$在其定义域内是减函数
②函数y=x2-2x的零点只有两个
③若函数f(2x)的定义域为[1,2],则函数f(2x)的定义域为[1,2]
④若函数f(x)=lg(x2+mx+1)(m∈R)的值域为R,则实数m的取值范围为(-∞,-2]∪[2,+∞),其中说法正确的序号是③④.(请把正确的序号全部写上)
分析 ①函数$y=\frac{1}{x}$在其定义域(-∞,0)∪(0,+∞)内不具有单调性,即可判断出正误;
②函数y=x2-2x的图象如图所示,即可判断出正误;
③由若函数f(2x)的定义域为[1,2],可得1≤x≤2,因此2≤2x≤4,由2≤2x≤4,解出即可判断出正误;
④由函数f(x)=lg(x2+mx+1)(m∈R)的值域为R,△=m2-4≥0,解得m≤-2,或m≥2,因此则实数m的
解答 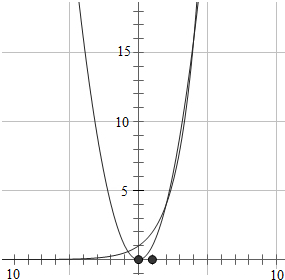 解:①函数$y=\frac{1}{x}$在其定义域(-∞,0)∪(0,+∞)内不具有单调性,因此不正确;
解:①函数$y=\frac{1}{x}$在其定义域(-∞,0)∪(0,+∞)内不具有单调性,因此不正确;
②函数y=x2-2x的图象如图所示,
零点有三个,因此不正确.
③若函数f(2x)的定义域为[1,2],∴1≤x≤2,∴2≤2x≤4,由2≤2x≤4,解得1≤x≤2,因此则函数f(2x)的定义域为[1,2],正确;
④若函数f(x)=lg(x2+mx+1)(m∈R)的值域为R,△=m2-4≥0,解得m≤-2,或m≥2,因此则实数m的取值范围为(-∞,-2]∪[2,+∞),正确.
其中说法正确的序号是③④.
故答案为:③④.
点评 本题考查了函数的图象与性质、函数的定义域与值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.$f(x)=\left\{\begin{array}{l}{(3-a)x+1\\;x<1}\\{{a}^{x}\\;x≥1}\end{array}\right.$,满足对任意x1≠x2,都有$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0成立,那么a的取值范围是( )
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (1,+∞) |
15.函数y=x0-$\sqrt{1-2x}$的定义域是( )
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,0)∪(0,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,+∞) |
16.为了对某课题进行研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人)
(Ⅰ)求x,y;
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这2人都来自高校C的概率.
| 高校 | 相关人数 | 抽取人数 |
| A | 15 | 1 |
| B | 30 | x |
| C | 60 | y |
(Ⅱ)若从高校B、C抽取的人中选2人作专题发言,求这2人都来自高校C的概率.
17.函数f(x)=x3+x-1在下列哪个区间内有零点?( )
| A. | (-1,0) | B. | (1,2) | C. | (0,1) | D. | (2,3) |