题目内容
3.若g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$+cos(x-$\frac{π+1}{2}$),则g($\frac{1}{2017}$)+g($\frac{2}{2017}$)+g($\frac{3}{2017}$)+g($\frac{4}{2017}$)+…+g($\frac{2016}{2017}$)的值为2016.分析 先化简g(x),得到g(x)+g(1-x)=2,进行求解即可.
解答 解:g(x)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$+cos(x-$\frac{π}{2}$-$\frac{1}{2}$)=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$+sin(x-$\frac{1}{2}$),
则g($\frac{1}{2}$+x)=$\frac{1}{3}$($\frac{1}{2}$+x)3-$\frac{1}{2}$($\frac{1}{2}$+x)2+3($\frac{1}{2}$+x)-$\frac{5}{12}$+sin($\frac{1}{2}$+x-$\frac{1}{2}$)=$\frac{1}{3}$($\frac{1}{2}$+x)3-$\frac{1}{2}$($\frac{1}{2}$+x)2+3($\frac{1}{2}$+x)-$\frac{5}{12}$+sinx,
g($\frac{1}{2}$-x)=$\frac{1}{3}$($\frac{1}{2}$-x)3-$\frac{1}{2}$($\frac{1}{2}$-x)2+3($\frac{1}{2}$-x)-$\frac{5}{12}$+sin($\frac{1}{2}$-x-$\frac{1}{2}$)=$\frac{1}{3}$($\frac{1}{2}$-x)3-$\frac{1}{2}$($\frac{1}{2}$-x)2+3($\frac{1}{2}$-x)-$\frac{5}{12}$-sinx,
则g($\frac{1}{2}$+x)+g($\frac{1}{2}$-x)=$\frac{1}{3}$[($\frac{1}{2}$+x)3+($\frac{1}{2}$-x)3]-$\frac{1}{2}$[($\frac{1}{2}$+x)2+($\frac{1}{2}$-x)2)]+3[($\frac{1}{2}$+x)+($\frac{1}{2}$-x)]-$\frac{5}{6}$
=$\frac{1}{3}$[($\frac{1}{2}$+x)3+($\frac{1}{2}$-x)3]-$\frac{1}{2}$[($\frac{1}{2}$+x)2+($\frac{1}{2}$-x)2)]+3[($\frac{1}{2}$+x)+($\frac{1}{2}$-x)]-$\frac{5}{6}$
=$\frac{1}{3}$[2×($\frac{1}{2}$)3+3×x2]-$\frac{1}{2}$($\frac{1}{2}$+2x2)+3×1-$\frac{5}{6}$
=$\frac{1}{12}$+x2-$\frac{1}{4}$-x2+3×1-$\frac{5}{6}$=3+$\frac{1}{12}$-$\frac{1}{4}$-$\frac{5}{6}$=3-1=2,
即g($\frac{1}{2}$+x)+g($\frac{1}{2}$-x)=2,
则g(x)+g(1-x)=2,
设g($\frac{1}{2017}$)+g($\frac{2}{2017}$)+g($\frac{3}{2017}$)+…+g($\frac{2015}{2017}$)+g($\frac{2016}{2017}$)=S,
则g($\frac{2016}{2017}$)+g($\frac{2015}{2017}$)+g($\frac{2014}{2017}$)+…+g($\frac{2}{2017}$)+g($\frac{1}{2017}$)=S,
即2S=2016[g($\frac{1}{2017}$)+g($\frac{2016}{2017}$)]=2016×2,
则S=2016,
故答案为:2016
点评 本题主要考查函数值的计算,根据条件得到g(x)+g(1-x)=2是解决本题的关键.综合性较强,运算比较复杂.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | -$\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
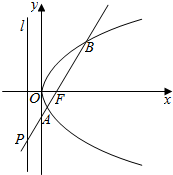 已知抛物线C:y2=2px(p>0)焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线l于P点.
已知抛物线C:y2=2px(p>0)焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线l于P点.