题目内容
 直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=
直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以A为原点,AB为x轴,AA1为y轴,以AC为z轴,建立空间直角坐标系,利用向量法能求出直线AC1与直线A1B夹角的余弦值.
解答:
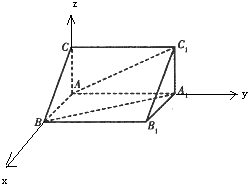 解:∵直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=
解:∵直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=
,
∴以A为原点,AB为x轴,AA1为y轴,以AC为z轴,
建立空间直角坐标系,
设AB=AA1=2CA=2,
则A(0,0,0),C1(0,2,1)
A1(0,2,0),B(2,0,0),
∴
=(0,2,1),
=(2,-2,0),
cos<
,
>=
=-
.
∴直线AC1与直线A1B夹角的余弦值为
.
故选:C.
 解:∵直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=
解:∵直三棱柱ABC-A1B1C1中,AB=AA1=2CA,∠CAB=| π |
| 2 |
∴以A为原点,AB为x轴,AA1为y轴,以AC为z轴,
建立空间直角坐标系,
设AB=AA1=2CA=2,
则A(0,0,0),C1(0,2,1)
A1(0,2,0),B(2,0,0),
∴
| AC1 |
| A1B |
cos<
| AC1 |
| A1B |
| -4 | ||||
|
| ||
| 5 |
∴直线AC1与直线A1B夹角的余弦值为
| ||
| 5 |
故选:C.
点评:本题考查异面直线所成角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
棱长都是1的三棱锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}的通项公式为an=
(n=1,2,…,),Sn是数列{an}的前n项和,则Sn=( )
| 1 | ||||
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=(x2-2x)ex,x∈[-2,+∞),f′(x)是函数f(x)的导函数,且f′(x)有两个零点x1和x2(x1<x2),则f(x)的最小值为( )
| A、f(x1) |
| B、f(x2) |
| C、f(-2) |
| D、以上都不对 |
顶点在原点,焦点在y轴上,其上点P(m,-3)到焦点距离为5,则抛物线的方程( )
| A、x2-8y=0 |
| B、x2+8y=0 |
| C、8x2-y=0 |
| D、8x2+y=0 |
下列函数中,定义域为(0,+∞)的函数是( )
| A、y=ex | ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|