题目内容
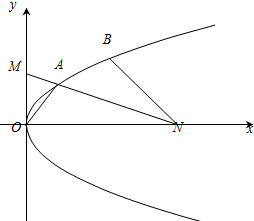如图，已知抛物线C：y2=2px（p＞0）上有两个动点A，B，它们的横坐标分别为a，a+2，当a=1时，点A到x轴的距离为| 2 |
（Ⅰ）求抛物线C的方程；
（Ⅱ）若A，B在x轴上方，且|OA|=|OM|，直线MA交x轴于N，求证：直线BN的斜率为定值，并求出该定值．
考点：抛物线的简单性质
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）求出A的坐标，代入，即可求抛物线C的方程；
（Ⅱ）求得直线MA的方程，可得N的坐标，即可证明直线BN的斜率为定值，并求出该定值．
（Ⅱ）求得直线MA的方程，可得N的坐标，即可证明直线BN的斜率为定值，并求出该定值．
解答：
（Ⅰ）解：由题意得当a=1时，点A坐标为(1，±
)，
由题有(±
)2=2p，∴p=1
∴抛物线C的方程为：y2=2x
（Ⅱ）证明：由题A(a，
)，B(a+2，
)，
∵|OA|=|OM|，
∴M(0，
)，
∴kMA=
∴直线MA的方程为：y=
x+
，
∴xN=
=
∴kBN=
=
=
=
=-1，
∴直线BN的斜率为定值，该定值为-1．
| 2 |
由题有(±
| 2 |
∴抛物线C的方程为：y2=2x
（Ⅱ）证明：由题A(a，
| 2a |
| 2a+4 |
∵|OA|=|OM|，
∴M(0，
| a2+2a |
∴kMA=
| ||||
| -a |
∴直线MA的方程为：y=
| ||||
| -a |
| a2+2a |
∴xN=
a
| ||||
|
a
| ||||
|
∴kBN=
| ||||||||
a+2-
|
| ||||||||
|
=
| ||||||
|
| ||||||
2-
|
∴直线BN的斜率为定值，该定值为-1．
点评：本题考查抛物线方程，考查直线斜率的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目