题目内容
若60<x<84,28<y<33,则x-y的取值范围是 .
的取值范围是 .
| x |
| y |
考点:不等关系与不等式,基本不等式
专题:不等式的解法及应用
分析:由题意可得-33<-y<-28,
<
<
,由不等式的可加性和可乘性可得.
| 1 |
| 33 |
| 1 |
| y |
| 1 |
| 28 |
解答:
解:∵60<x<84,28<y<33,
∴-33<-y<-28,
<
<
,
∴60-33<x-y<84-28,即27<x-y<56,
∴
<
<
,即
<
<3,
故答案为:(27,56);(
,3)
∴-33<-y<-28,
| 1 |
| 33 |
| 1 |
| y |
| 1 |
| 28 |
∴60-33<x-y<84-28,即27<x-y<56,
∴
| 60 |
| 33 |
| x |
| y |
| 84 |
| 28 |
| 20 |
| 11 |
| x |
| y |
故答案为:(27,56);(
| 20 |
| 11 |
点评:本题考查不等式的性质,属基础题.

练习册系列答案
相关题目
动圆M经过双曲线x2-
=1的左焦点且与直线x=2相切,则圆心M的轨迹方程是( )
| y2 |
| 3 |
| A、y2=8x |
| B、y2=-8x |
| C、y2=4x |
| D、y2=-4x |
函数y=cos2x+cosx的最小值是( )
| A、-1 | ||
B、-
| ||
| C、0 | ||
D、
|
已知命题P:?a,b(0,+∞),当a+b=1时,
+
=3; 命题Q:?x∈R,x2-x+1≥0恒成立,则下列命题是假命题的是( )
| 1 |
| a |
| 1 |
| b |
| A、¬P∨¬Q | B、¬P∧¬Q |
| C、¬P∨Q | D、¬P∧Q |
在△ABC中,a=8,B=60°,c=4(
+1),则b等于( )
| 3 |
A、2
| ||
B、4
| ||
C、4(
| ||
D、4
|
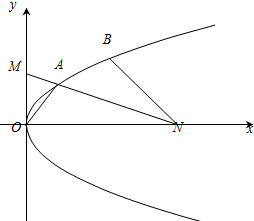 如图,已知抛物线C:y2=2px(p>0)上有两个动点A,B,它们的横坐标分别为a,a+2,当a=1时,点A到x轴的距离为
如图,已知抛物线C:y2=2px(p>0)上有两个动点A,B,它们的横坐标分别为a,a+2,当a=1时,点A到x轴的距离为