题目内容
已知数列{an}满足:a1=1,4an+1=5an+
.
(1)计算a2,a3,a4,猜想求数列{an}的通项公式,并给与证明;
(2)证明:
+
+…+
<2.
| 9an2+16 |
(1)计算a2,a3,a4,猜想求数列{an}的通项公式,并给与证明;
(2)证明:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
考点:数学归纳法,归纳推理
专题:综合题,点列、递归数列与数学归纳法
分析:(1)写出前四项猜出一个符合的通项公式,然后利用数学归纳法进行证明;
(2)取倒数,利用放缩法,结合等比数列的求和公式即可得出结论.
(2)取倒数,利用放缩法,结合等比数列的求和公式即可得出结论.
解答:
(1)解:∵a1=1,4an+1=5an+
,
∴a2=
,a3=
,a4=
,
猜想an=
;
证明如下:①n=1时,a1=1;
②假设n=k时,结论成立,则
n=k+1时,4ak+1=5ak+
,
∴ak+1=
ak+
=
•
+
=
.
即n=k+1时,结论成立,
由①②可知,an=
;
(2)证明:∵an=
,
∴
=
=
•
<
•
,
∴
+
+…+
<
(
+
+…+
)=
(1-
)<2.
| 9an2+16 |
∴a2=
| 5 |
| 2 |
| 21 |
| 4 |
| 85 |
| 8 |
猜想an=
| 4n-1 |
| 3•2n-1 |
证明如下:①n=1时,a1=1;
②假设n=k时,结论成立,则
n=k+1时,4ak+1=5ak+
| 9ak2+16 |
∴ak+1=
| 5 |
| 4 |
| 1 |
| 4 |
| 9ak2+16 |
| 5 |
| 4 |
| 4k-1 |
| 3•2k-1 |
| 1 |
| 4 |
9•(
|
| 4k+1-1 |
| 3•2k |
即n=k+1时,结论成立,
由①②可知,an=
| 4n-1 |
| 3•2n-1 |
(2)证明:∵an=
| 4n-1 |
| 3•2n-1 |
∴
| 1 |
| an |
| 3•2n-1 |
| 4n-1 |
| 3 |
| 2 |
| 2n |
| 4n-1 |
| 3 |
| 2 |
| 1 |
| 2n |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| 3 |
| 2 |
| 1 |
| 2n |
点评:本题主要考查了数学归纳法证明,关键在于n=k+1时的运算要做到有的放矢.

练习册系列答案
相关题目
已知数列{an}满足a1=0,an+1=an+2n,那么a2009的值是( )
| A、20092 |
| B、2008×2007 |
| C、2009×2010 |
| D、2008×2009 |
已知命题P:?a,b(0,+∞),当a+b=1时,
+
=3; 命题Q:?x∈R,x2-x+1≥0恒成立,则下列命题是假命题的是( )
| 1 |
| a |
| 1 |
| b |
| A、¬P∨¬Q | B、¬P∧¬Q |
| C、¬P∨Q | D、¬P∧Q |
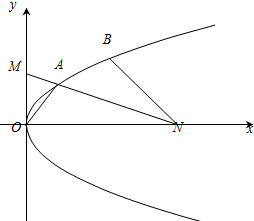 如图,已知抛物线C:y2=2px(p>0)上有两个动点A,B,它们的横坐标分别为a,a+2,当a=1时,点A到x轴的距离为
如图,已知抛物线C:y2=2px(p>0)上有两个动点A,B,它们的横坐标分别为a,a+2,当a=1时,点A到x轴的距离为