题目内容
15.命题“若$\frac{{{a_n}+{a_{n+2}}}}{2}<{a_{n+1}}\;(n∈{{N}^*})$,则数列{an}为递减数列”的逆否命题是若数列数列{an}不为递减数列,则$\frac{{a}_{n}+{a}_{n+2}}{2}$≥an+1,n∈N*.分析 根据若p则q的逆否命题是若¬q则¬p,写出其逆否命题即可.
解答 解:命题“若$\frac{{{a_n}+{a_{n+2}}}}{2}<{a_{n+1}}\;(n∈{{N}^*})$,则数列{an}为递减数列”的逆否命题是:
若数列数列{an}不为递减数列,则$\frac{{a}_{n}+{a}_{n+2}}{2}$≥an+1,n∈N*,
故答案为:若数列数列{an}不为递减数列,则$\frac{{a}_{n}+{a}_{n+2}}{2}$≥an+1,n∈N*
点评 本题考查了四种命题之间的关系,熟练掌握四种命题在关系是解题的关键,本题属于基础题.

练习册系列答案
相关题目
6.以点A(-3,4)为圆心,且与y轴相切的圆的标准方程为( )
| A. | (x+3)2+(y-4)2=16 | B. | (x-3)2+(y+4)2=16 | C. | (x+3)2+(y-4)2=9 | D. | (x-3)2+(y+4)2=9 |
10.已知△ABC的三个内角A,B,C满足2017cos2C-cos2A=2016-2sin2B,则$\frac{tanC•(tanA+tanB)}{tanA•tanB}$=( )
| A. | $\frac{2017}{2}$ | B. | $\frac{2}{2017}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{1008}$ |
7.将参数方程$\left\{\begin{array}{l}x=2+sin2θ\\ y=sin2θ\end{array}$(θ为参数)化为普通方程是( )
| A. | y=x-2 | B. | y=x+2 | C. | y=x-2(1≤x≤3) | D. | y=x+2(0≤y≤1) |
5.已知f(x)=2x-2-x,a=($\frac{7}{9}$)${\;}^{-\frac{1}{4}}$,b=($\frac{9}{7}$)${\;}^{\frac{1}{5}}$,c=log2$\frac{7}{9}$,则f(a),f(b),f(c)的大小顺序为( )
| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
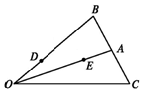 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$ 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.