题目内容
已知函数f(x)=x(x-a)(x-b),点A(s,f(s)),B(t,f(t)).
(Ⅰ)若a=0,b=3,函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,求t的取值范围;
(Ⅱ)当a=0时,
+lnx+1≥0对任意的x∈[
,+∞)恒成立,求b的取值范围;
(Ⅲ)若0<a<b,函数f(x)在x=s和x=t处取得极值,且a+b<2
,O是坐标原点,探究直线OA与直线OB能否垂直,并说明理由.
(Ⅰ)若a=0,b=3,函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,求t的取值范围;
(Ⅱ)当a=0时,
| f(x) |
| x |
| 1 |
| 2 |
(Ⅲ)若0<a<b,函数f(x)在x=s和x=t处取得极值,且a+b<2
| 3 |
考点:导数在最大值、最小值问题中的应用,函数恒成立问题,函数在某点取得极值的条件
专题:导数的综合应用
分析:(Ⅰ)直接求导得f'(x)=3x2-6x,令f'(x)=0即可确定极值点,解不等式t<0且t+3>2即可求解t的取值范围;
(Ⅱ)化简
+lnx+1≥0得b≤x+
+
,然后求函数g(x)=x+
+
在x∈[
,+∞)的最小值,即可确定b的取值范围;
(Ⅲ)假设直线OA与直线OB垂直,运用数量积的坐标运算建立s,t的方程,根据极值的性质可知s,t是方程f'(x)=0的两个根,从而确定a+b的值,得出与已知的矛盾,推翻假设.得出结论.
(Ⅱ)化简
| f(x) |
| x |
| lnx |
| x |
| 1 |
| x |
| lnx |
| x |
| 1 |
| x |
| 1 |
| 2 |
(Ⅲ)假设直线OA与直线OB垂直,运用数量积的坐标运算建立s,t的方程,根据极值的性质可知s,t是方程f'(x)=0的两个根,从而确定a+b的值,得出与已知的矛盾,推翻假设.得出结论.
解答:
(Ⅰ)当a=0,b=3时,
f(x)=x3-3x2,f'(x)=3x2-6x,
令f'(x)=0得,x=0或x=2.
根据导数的符号可知,
函数f(x)在x=0处取得极大值,在x=2处取得极小值.
∵函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,
∴t<0且t+3>2,
即-1<t<0.
∴t的取值范围是(-1,0).
(Ⅱ)当a=0时,
+lnx+1≥0对任意的x∈[
,+∞)恒成立,
即x2-bx+lnx+1≥0对任意的x∈[
,+∞)恒成立,
即b≤x+
+
在对任意的x∈[
,+∞)恒成立.
令g(x)=x+
+
,
则g′(x)=1+
-
=
.
记m(x)=x2-lnx,
则m′(x)=2x-
=
,
则这个函数在其定义域内有唯一的极小值点x=
,
并且也是最小值点,
∴m(x)≥m(
)=
-ln
>0,
从而g'(x)>0,
∴函数g(x)在区间[
,+∞)上单调递增.
函数g(x)min=g(
)=
-2ln2.
故只要b≤
-2ln2即可.
∴b的取值范围是(-∞,
-2ln2].
(Ⅲ)假设
⊥
,即
•
=0,
即(s,f(s))•(t,f(t))=st+f(s)f(t)=0,
故(s-a)(s-b)(t-a)(t-b)=-1.
即[st-(s+t)a+a2][st-(s+t)b+b2]=-1.
由于s,t是方程f'(x)=0的两个根,
故s+t=
(a+b),st=
,0<a<b.
代入上式得ab(a-b)2=9.
(a+b)2=(a-b)2+4ab=
+4ab≥2
=12,
即a+b≥2
,与a+b<2
矛盾,
∴直线OA与直线OB不可能垂直.
f(x)=x3-3x2,f'(x)=3x2-6x,
令f'(x)=0得,x=0或x=2.
根据导数的符号可知,
函数f(x)在x=0处取得极大值,在x=2处取得极小值.
∵函数f(x)在(t,t+3)上既能取到极大值,又能取到极小值,
∴t<0且t+3>2,
即-1<t<0.
∴t的取值范围是(-1,0).
(Ⅱ)当a=0时,
| f(x) |
| x |
| 1 |
| 2 |
即x2-bx+lnx+1≥0对任意的x∈[
| 1 |
| 2 |
即b≤x+
| lnx |
| x |
| 1 |
| x |
| 1 |
| 2 |
令g(x)=x+
| lnx |
| x |
| 1 |
| x |
则g′(x)=1+
| 1-lnx |
| x2 |
| 1 |
| x2 |
| x2-lnx |
| x2 |
记m(x)=x2-lnx,
则m′(x)=2x-
| 1 |
| x |
| 2x2-1 |
| x |
则这个函数在其定义域内有唯一的极小值点x=
| ||
| 2 |
并且也是最小值点,
∴m(x)≥m(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
从而g'(x)>0,
∴函数g(x)在区间[
| 1 |
| 2 |
函数g(x)min=g(
| 1 |
| 2 |
| 5 |
| 2 |
故只要b≤
| 5 |
| 2 |
∴b的取值范围是(-∞,
| 5 |
| 2 |
(Ⅲ)假设
| OA |
| OB |
| OA |
| OB |
即(s,f(s))•(t,f(t))=st+f(s)f(t)=0,
故(s-a)(s-b)(t-a)(t-b)=-1.
即[st-(s+t)a+a2][st-(s+t)b+b2]=-1.
由于s,t是方程f'(x)=0的两个根,
故s+t=
| 2 |
| 3 |
| ab |
| 3 |
代入上式得ab(a-b)2=9.
(a+b)2=(a-b)2+4ab=
| 9 |
| ab |
| 36 |
即a+b≥2
| 3 |
| 3 |
∴直线OA与直线OB不可能垂直.
点评:本题主要考查向量的数量积的性质和坐标运算,导数与极值最值的关系,恒成立问题的解决技巧等知识的综合应用,属于难题.

练习册系列答案
相关题目
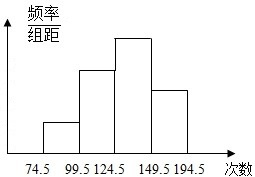 为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:
为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题: 函数
函数 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).