题目内容
8.若$\frac{sinα}{\sqrt{1-co{s}^{2}α}}$=$\frac{cosα}{\sqrt{1-si{n}^{2}α}}$,则角α是( )| A. | 第一象限 | B. | 第三象限 | ||
| C. | 第一象限或第三象限 | D. | 第二象限或第四象限 |
分析 根据同角的三角函数关系即可求出.
解答 解:$\frac{sinα}{\sqrt{1-co{s}^{2}α}}$=$\frac{cosα}{\sqrt{1-si{n}^{2}α}}$,
则$\frac{sinα}{|sinα|}$=$\frac{cosα}{|cosα|}$,
∴角α是第一象限或第三象限,
故选:C.
点评 本题考查了同角三角函数的关系,以及象限角的符号,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+4b的取值范围是( )
| A. | (4,+∞) | B. | [4,+∞) | C. | (5,+∞) | D. | [5,+∞) |
2.若实数x,y满足$\left\{\begin{array}{l}{\sqrt{3}x-y≥0}\\{x-2y≤0}\\{(x-1)^{2}+{y}^{2}≤1}\end{array}\right.$,则y的最大值为( )
| A. | $\sqrt{3}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{4}{5}$ |
 如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.
如图,在三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面BB1C1C,AC⊥CC1.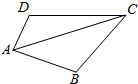 如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.
如图所示,已知四边形ABCD各边的长分别为AB=5,BC=5,CD=8,DA=3,且点A、B、C、D在同一个圆上,则对角线AC的长为$\frac{55}{7}$.