题目内容
已知集合A={x∈R|x2-2x-3≤0}，B={x∈R|
＜1}，则A∩B= ．
| 1 |
| x |
考点：交集及其运算
专题：集合
分析：求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．
解答：
解：由A中的不等式变形得：（x-3）（x+1）≤0，
解得：-1≤x≤3，即A=[-1，3]；
当x＜0时，B中不等式去分母得：x＜1，即B=（-∞，0）；
当x＞0时，B中不等式去分母得：x＞1，即B=（1，+∞），
∴B=（-∞，0）∪（1，+∞），
∴A∩B=[-1，0）∪（1，3]．
故答案为：[-1，0）∪（1，3]
解得：-1≤x≤3，即A=[-1，3]；
当x＜0时，B中不等式去分母得：x＜1，即B=（-∞，0）；
当x＞0时，B中不等式去分母得：x＞1，即B=（1，+∞），
∴B=（-∞，0）∪（1，+∞），
∴A∩B=[-1，0）∪（1，3]．
故答案为：[-1，0）∪（1，3]
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
设f（
）=x，则f′（x）=（ ）
| 1 |
| x |
| A、1 | ||
B、
| ||
C、-
| ||
| D、2x |
设U=R，若集合M={x|-1＜x≤2}，则∁UM=（ ）
| A、（-∞，-1] |
| B、（2，+∞） |
| C、（-∞，-1]∪[2，+∞） |
| D、（-∞，-1]∪（2，+∞） |
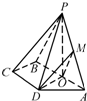如图，已知四棱锥P-ABCD，底面ABCD是等腰梯形，且AB∥CD，O是AB中点，PO⊥平面ABCD，PO=CD=DA=