题目内容
10.已知数列{an}是公差为2的等差数列,数列{bn}满足${b_1}=1,{b_2}=\frac{1}{2}$,若n∈N*时,anbn+1-bn+1=nbn.(Ⅰ)求{bn}的通项公式;
(Ⅱ)设cn=anbn,求{cn}的前n项和Sn.
分析 (I)由数列{bn}满足${b_1}=1,{b_2}=\frac{1}{2}$,anbn+1-bn+1=nbn.n=1时,可得a1b2-b2=b1,即$\frac{1}{2}{a}_{1}$-$\frac{1}{2}$=1,解得a1.可得an=2n+1.代入anbn+1-bn+1=nbn.利用等比数列的通项公式即可得出.
(II)cn=anbn=(2n+1)×$(\frac{1}{2})^{n-1}$.利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(I)∵数列{bn}满足${b_1}=1,{b_2}=\frac{1}{2}$,anbn+1-bn+1=nbn.∴n=1时,可得a1b2-b2=b1,
即$\frac{1}{2}{a}_{1}$-$\frac{1}{2}$=1,解得a1=3.
∴an=3+2(n-1)=2n+1.
∴[(2n+1)-1]bn+1=nbn,可得bn+1=$\frac{1}{2}$bn,
∴数列{bn}是等比数列,公比为$\frac{1}{2}$.
∴bn=$(\frac{1}{2})^{n-1}$.
(II)cn=anbn=(2n+1)×$(\frac{1}{2})^{n-1}$.
∴{cn}的前n项和Sn=$3×1+5×\frac{1}{2}$+7×$(\frac{1}{2})^{2}$+…+(2n+1)×$(\frac{1}{2})^{n-1}$.
∴$\frac{1}{2}{S}_{n}$=$3×\frac{1}{2}+5×(\frac{1}{2})^{2}$+…+(2n-1)×$(\frac{1}{2})^{n-1}$+(2n+1)×$(\frac{1}{2})^{n}$,
∴$\frac{1}{2}{S}_{n}$=3+$2(\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}})$-(2n+1)×$(\frac{1}{2})^{n}$=1+$2×\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-(2n+1)×$(\frac{1}{2})^{n}$,
∴Tn=10-$\frac{2n+5}{{2}^{n-1}}$
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案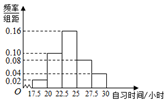 某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140.
某中学调查200名学生每周晚自习时间(单位,小时),制成了如图所示频率分布直方图,其中自习时间的范围为[17.5,30],根据直方图,这200名学生每周自习时间不少于22.5小时的人数是140. | A. | 135° | B. | 120° | C. | 60° | D. | 45° |
| A. | {-2,-1,0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
| A. | $\frac{3}{4}-\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{3}{4}+\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
 一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.