题目内容
10.若函数f(x)=2sin($\frac{1}{2}$x+$\frac{4φ}{3}$)(φ∈($\frac{π}{2}$,π)的图象向左平移$\frac{2π}{3}$个单位长度得到函数g(x)的图象,且函数g(x)是偶函数,则φ的值为$\frac{7π}{8}$.分析 由条件利用y=Asin(ωx+φ)的图象变换规律,三角函数的奇偶性,求得φ的值.
解答 解:把函数f(x)=2sin($\frac{1}{2}$x+$\frac{4φ}{3}$)(φ∈($\frac{π}{2}$,π)的图象向左平移$\frac{2π}{3}$个单位长度,
得到函数g(x)=2sin[$\frac{1}{2}$(x+$\frac{2π}{3}$)+$\frac{4φ}{3}$]=2sin($\frac{1}{2}$x+$\frac{4φ}{3}$+$\frac{π}{3}$)的图象.
再根据函数g(x)是偶函数,可得$\frac{4φ}{3}$+$\frac{π}{3}$=kπ+$\frac{π}{2}$,即φ=$\frac{3kπ}{4}$+$\frac{π}{8}$,k∈Z,
故φ=$\frac{7π}{8}$,
故答案为:$\frac{7π}{8}$.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,三角函数的奇偶性,属于基础题.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目
18.已知集合A={x|x2-3x+2>0},集合B={y|y=2cosx+1},则(∁RA)∩B=( )
| A. | (-∞,-1)∪(2,+∞) | B. | [1,2] | C. | [-1,1)∪(2,3] | D. | [-1,3] |
5.已知函数f(x)=$\frac{x}{x+1}$+2x-mln(x+1)在(0,+∞)上是增函数,则实数m的取值范围为( )
| A. | (-∞,2$\sqrt{2}$] | B. | (-∞,2$\sqrt{2}$) | C. | (-∞,3) | D. | (-∞,3] |
15.通过随机询问110名性别不同的大学生是否爱好体育,得到如表的列联表:
由公式算得:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}≈7.8$
附表:
参照附表,得到的正确结论是( )
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
附表:
| P(K2≥K0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有99%以上的把握认为“爱好体育运动与性别有关” | |
| B. | 有99%以上的把握认为“爱好体育运动与性别无关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别有关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好体育运动与性别无关” |
2.设函数f(x)=|2x-1|,c<b<a,且f(c)>f(a)>f(b),则下列关系式正确的是( )
| A. | a+c≤0 | B. | a+c>0 | C. | a+c≤0 | D. | a+c<0 |
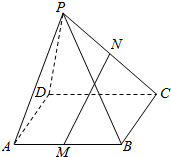 如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是平行四边形,三角形ADP中AD=AP=5,PD=6,M、N分别是AB,PC的中点.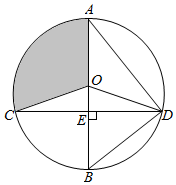 如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.