题目内容
1.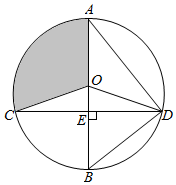 如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.
如图,已知⊙O的直径AB垂直于弦CD于E,连结 AD、BD、OC、OD,且 OD=5.(1)求证:∠CDB=∠ADO;
(2)若sin∠BAD=$\frac{3}{5}$,求 CD 的长.
分析 (1)根据圆周角定理,以及三角形全等即可证明.
(2)由⊙O的直径AB垂直于弦CD于E,利用垂径定理可得CE=ED.在Rt△ABD中,利用直角三角形的边角关系可得BD=ABsin∠BAD.再利用勾股定理可得.由等面积变形可得,即可得出.
解答  证明:(1)因为AB是⊙O的直径,AB⊥CD,
证明:(1)因为AB是⊙O的直径,AB⊥CD,
所以$\widehat{CB}$=$\widehat{BD}$,$\widehat{AC}$=$\widehat{AD}$,所以∠BAD=∠CDB,…(2分)
∠AOC=∠AOD.因为AO=DO,所以∠BAD=∠ADO,
所以∠CDB=∠ADO.…(5分)
(2)因为AB是⊙O的直径,OD=5
所以∠ADB=90°,AB=10
在Rt△ABD中,$sin∠BAD=\frac{BD}{AB}$
又$sin∠BAD=\frac{3}{5}$,所以$\frac{BD}{10}=\frac{3}{5}$,
所以BD=6.…(7分)$AD=\sqrt{A{B^2}-B{D^2}}=\sqrt{{{10}^2}-{6^2}}=8$
因为∠ADB=90°,AB⊥CD
所以$DE\cdotAB=AD\cdotBD,CE=DE$
所以DE×10=8×6
所以$DE=\frac{24}{5}$,所以$CD=2DE=\frac{48}{5}$.…(10分)
点评 本题综合考查了圆的性质、垂径定理、直角三角形的边角关系、勾股定理、等面积变形、三角形外角定理、扇形的面积计算公式等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
11.下列问题中,应采用哪种抽样方法( )
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
①有甲厂生产的30个篮球,其中一箱21个,另一箱9个,抽取10个入样;
②有30个篮球,其中甲厂生产的有21个,乙厂生产的有9个,抽取10个入样;
③有甲厂生产的300个篮球,抽取10个入样;
④有甲厂生产的300 个篮球,抽取50个入样.
| A. | 分层抽样、分层抽样、抽签法、系统抽样 | |
| B. | 分层抽样、分层抽样、随机数法、系统抽样 | |
| C. | 抽签法、分层抽样、随机数法、系统抽样 | |
| D. | 抽签法、分层抽样、系统抽样、随机数法 |
12.△ABC的内角A、B、C的对边分别为a,b,c,且a:b:c=$\sqrt{13}$:4:3,设$\overrightarrow{m}$=$\overrightarrow{AB}$cosA,$\overrightarrow{n}$=$\overrightarrow{AC}$sinA,又△ABC的面积为S,则$\overrightarrow{m}$•$\overrightarrow{n}$=( )
| A. | $\frac{\sqrt{13}}{2}$S | B. | $\frac{3}{2}$S | C. | S | D. | $\frac{1}{2}$S |
11.若直线l:ax+y-2-a=0在x轴和y轴上的截距相等,则直线l的斜率为( )
| A. | 1 | B. | -1 | C. | -2或1 | D. | -1或-2 |