题目内容
利用函数f(x)=(
)x+(
)x(x∈R)是减函数可以求方程(
)x+(
)x=1的解.由f(2)=1可知原方程有唯一解x=2,类比上述思路可知不等式x6-(x+2)>(x+2)3-x2的解集是 .
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
考点:类比推理
专题:计算题,推理和证明
分析:不等式x6-(x+2)>(x+2)3-x2等价为x6+x2>(x+2)3+(x+2).类比(
)x+(
)x=1,求方程的解的解题思路,设f(x)=x3+x,利用导数研究f(x)在R上单调递增,从而根据原方程可得x2>x+2,解之即得x6-(x+2)>(x+2)3-x2的解集.
| 3 |
| 5 |
| 4 |
| 5 |
解答:
解:∵不等式x6-(x+2)>(x+2)3-x2等价为x6+x2>(x+2)3+(x+2).
∴设f(x)=x3+x,
则函数f(x)在R上单调递增,
由x6+x2>(x+2)3+(x+2),
即(x2)3+x2>(x+2)3+(x+2),
∴x2>x+2,
解得x<-1或x>2.
∴不等式x6-(x+2)>(x+2)3-x2的解集是{x|x<-1或x>2}.
故答案为:{x|x<-1或x>2}.
∴设f(x)=x3+x,
则函数f(x)在R上单调递增,
由x6+x2>(x+2)3+(x+2),
即(x2)3+x2>(x+2)3+(x+2),
∴x2>x+2,
解得x<-1或x>2.
∴不等式x6-(x+2)>(x+2)3-x2的解集是{x|x<-1或x>2}.
故答案为:{x|x<-1或x>2}.
点评:本题主要考查了类比推理,考查了导数与单调性的关系,函数单调性的应用,考查学生分析问题,解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设T=|2x-1|,若不等式T(x)≥(1+
)-|2-
|对任意实数a≠0恒成立,则x的取值范围是( )
| 1 |
| a |
| 1 |
| a |
| A、(-∞,0]∪[1,+∞) |
| B、(0,1] |
| C、(-∞,-1]∪[2,+∞) |
| D、[-1,2] |
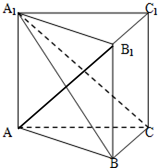 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.