题目内容
已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点,(1)若以AB为直径的圆过坐标原点,求实数a的值;(2)是否存在这样的实数a,使A、B两点关于直线y=
思路解析:(1)转化为OA⊥OB,即斜率之积为-1;(2)不妨假设存在,然后求值即可. 解:(1)由 依题意 设A(x1,y1),B(x2,y2),则 ∵以AB为直径的圆过原点,∴OA⊥OB.∴x1x2+y1y2=0. 但y1·y2=a2x1x2+a(x1+x2)+1, 由(3)(4),得x1+x2= ∴(a2+1)· (2)假设存在实数a,使A、B关于y= 将a=-2代入(3),得x1+x2=4,∴AB中点横坐标为2, 纵坐标为y=-2×2+1=-3.但AB中点(2,-3)不在直线y= 方法归纳 (1)直线与双曲线的关系问题,往往采用“设而不求”的方法,结合韦达定理求解;(2)开放性问题,则经常采用假设存在,直接推证的方法.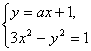 消去y,得(3-a2)x2-2ax-2=0. (1)
消去y,得(3-a2)x2-2ax-2=0. (1)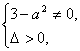 即-
即-![]() <a<
<a<![]() 且a≠±
且a≠±![]() . (2)
. (2)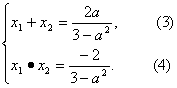
![]() ,x1x2=
,x1x2=![]() ,
,![]() +a·
+a·![]() +1=0.解得a=±1且满足(2).
+1=0.解得a=±1且满足(2).![]() x对称,则直线y=ax+1与y=
x对称,则直线y=ax+1与y=![]() x垂直,∴a=-2.直线l的方程为y=-2x+1.
x垂直,∴a=-2.直线l的方程为y=-2x+1.![]() x上,即不存在实数a使A、B关于直线y=
x上,即不存在实数a使A、B关于直线y=![]() x对称.
x对称.

新课程暑假作业本山西教育出版社系列答案
海淀黄冈名师暑假作业快乐假期吉林教育出版社系列答案
南方凤凰台假期之友暑假作业江苏凤凰教育出版社系列答案
暑假作业贵州科技出版社系列答案
Happy holiday快乐假期暑假电子科技大学出版社系列答案
暑假集训合肥工业大学出版社系列答案
暑假总复习暑假接力棒云南大学出版社系列答案
素质新目标暑假作业浙江人民出版社系列答案
暑假作业完美假期生活湖南教育出版社系列答案
暑假作业浙江科学技术出版社系列答案
 对称?说明理由。
对称?说明理由。