题目内容
已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点。
(1)若以AB线段为直径的圆过坐标原点,求实数a的值。
(2)是否存在这样的实数a,使A、B两点关于直线 对称?说明理由。
对称?说明理由。
【答案】
(1)联立方程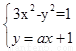 ,消去y得:(3-a2)x2-2ax-2=0.-------1分
,消去y得:(3-a2)x2-2ax-2=0.-------1分
设A(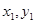 ),B(
),B(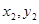 ),那么:
),那么: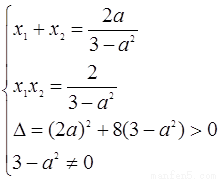 。--------3分
。--------3分
由于以AB线段为直径的圆经过原点,那么: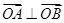 ,
,
即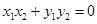 。
----------------------4分
。
----------------------4分
所以: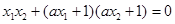 ,得到:
,得到: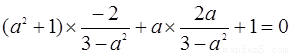
解得a=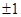 , ------------------5分
, ------------------5分
又根据题意a应该满足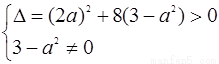
解得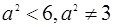 ,而a=
,而a=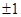 符合题意.
符合题意.
所以实数a=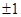 ------------------------------6分
------------------------------6分
(2)假定存在这样的a,使A(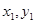 ),B(
),B(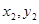 )关于直线
)关于直线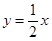 对称。
对称。
那么: ,
----------------8分
,
----------------8分
两式相减得: ,从而
,从而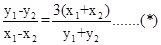 -------9分
-------9分
因为A(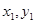 ),B(
),B(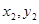 )关于直线
)关于直线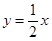 对称,
对称,
所以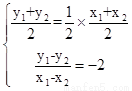 ------------12分
------------12分
代入(*)式得到:-2=6,矛盾。
也就是说:不存在这样的a,使A(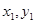 ),B(
),B(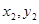 )关于直线
)关于直线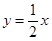 对称。
对称。
【解析】略

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目