题目内容
已知实数x,y满足约束条件
,则z=(x+1)2+y2的最小值是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义即可得到结论.
解答:
解:作出不等式组对应的平面区域,
则z的几何意义为区域内点P到点D(-1,0)的距离平方的最小值,
由图象可知,当DP垂直于直线x+2y-1=0时,
此时DP最小,|DP|=
=
,
则z=|DP|2=
,
故答案为:
则z的几何意义为区域内点P到点D(-1,0)的距离平方的最小值,

由图象可知,当DP垂直于直线x+2y-1=0时,
此时DP最小,|DP|=
| |-1+0-1| | ||
|
| 2 | ||
|
则z=|DP|2=
| 4 |
| 5 |
故答案为:
| 4 |
| 5 |
点评:本题主要考查线性规划的应用以及点到直线的距离公式的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
设函数f(x)的定义域为D,若f(x)满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域是[
,
],则成f(x)为“倍缩函数”,若函数f(x)=log2(2x+t)为“倍缩函数”,则t的范围是( )
| a |
| 2 |
| b |
| 2 |
A、(0,
| ||
| B、(0,1) | ||
C、(0,
| ||
D、(
|
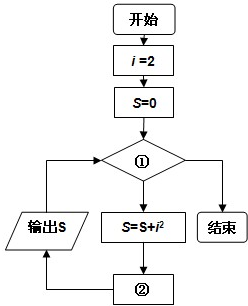 如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )
如图分别表示输出22,22+42,22+42+62,…,22+42+62+…+20142值得过程的一个程序框图,那么在图中①②分别填上( )| A、i≤2014,i=i+1 |
| B、i≤1007,i=i+1 |
| C、i≤2014,i=i+2 |
| D、i≤1007,i=i+2 |
 如图,在△ABC中,AB=BC,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,BD=4,CD=2
如图,在△ABC中,AB=BC,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,BD=4,CD=2 如图是某青年歌手大奖赛上七位评委为某选手打出的分数的茎叶图(其中m为数字0-9中的一个).若这组数据的中位数和平均数相等,则m=
如图是某青年歌手大奖赛上七位评委为某选手打出的分数的茎叶图(其中m为数字0-9中的一个).若这组数据的中位数和平均数相等,则m=