题目内容
8.已知线段AB的长为10,在线段AB上随机取两个点C、D,则|CD|>2的概率为( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{16}{25}$ |
分析 由已知中线段AB的长为10,在线段AB上随机取两个点C、D,设C、D坐标分别为x,y,则(x,y)点对应的平面区域为一个边长长为10的正方形,若|CD|>2,则|x-y|>2,求出满足条件的平面区域的面积,代入几可概型公式即可得到答案.
解答 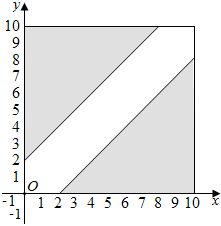 解:线段AB上随机取两个点C、D,设C、D坐标分别为x,y,
解:线段AB上随机取两个点C、D,设C、D坐标分别为x,y,
则(x,y)点对应的平面区域如下图所示:
其中满足|CD|>2的平面区域如图中阴影部分所示:
故|CD|>2的概率P=$\frac{{S}_{阴影}}{S{\;}_{正方形}}$=$\frac{64}{100}$=$\frac{16}{25}$,
故选:D.
点评 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=$\frac{N(A)}{N}$求解.

练习册系列答案
相关题目
16.某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化.每天各时刻t的浪高数据的平均值如下表:
(1)试在图中描出所给点;
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
13.设全集U=R,集合A={x|log2x≤2},$B=\left\{{x|\frac{4}{3-x}≥1}\right\}$,则A∩B=( )
| A. | [-1,3) | B. | (-∞,-1]∪(3,4] | C. | (0,3] | D. | (0,3) |
17.2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:
现从该港口随机抽取了n家公司,其中消防安全等级为三级的恰有20家.
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
| 等 级 | 一级 | 二级 | 三级 | 四级 |
| 频 率 | 0.30 | 2m | m | 0.10 |
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
18.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最小值为( )
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
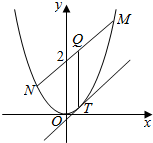 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.