题目内容
在海岸A处,发现北偏东45°方向,距离A( -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2n mile的C处的缉私船奉命以10 n mile/h的速度追截走私船.此时,走私船正以10n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
n mile/h的速度追截走私船.此时,走私船正以10n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
如图所示,注意到最快追上走私船且两船所用时间相等,若在D处相遇,则可先在△ABC中求出BC,再在△BCD中求∠BCD. 
设缉私船用th在D处追上走私船,则有CD=10 t,BD=10t,
t,BD=10t,
在△ABC中,∵AB= -1,AC=2,∠BAC=120°,
-1,AC=2,∠BAC=120°,
∴由余弦定理得
BC2=AB2+AC2-2AB·AC·cos∠BAC
=( -1)2+22-2·(
-1)2+22-2·( -1)·2·cos120°=6,
-1)·2·cos120°=6,
∴BC=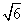 ,
,
∵cos∠CBA=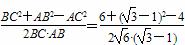 =
=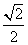 ,
,
∴∠CBA=45°,即B在C正东.
∵∠CBD=90°+30°=120°,
在△BCD中,由正弦定理得
sin∠BCD=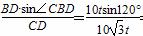 =
=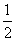 ,
,
∴∠BCD=30°.
即缉私船沿北偏东60°方向能最快追上走私船.

练习册系列答案
相关题目
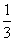 ,则cos2x-sin2y等于( )
,则cos2x-sin2y等于( ) D.
D. bc且b=
bc且b=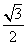 B.2-
B.2-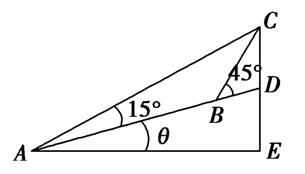
 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )
 D.
D. 
 ,则r+s的值是( )
,则r+s的值是( ) B.
B.
 ,则点B的坐标为________.
,则点B的坐标为________. B.2
B.2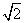
 D.
D.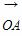 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),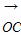 =(5-m,-3-m).
=(5-m,-3-m).