题目内容
13．已知复数$z=\frac{1+i}{i}$，其中i为虚数单位，则|z|=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | 2 |
分析 利用复数代数形式的乘除运算化简，再由复数模的计算公式求解．
解答 解：∵$z=\frac{1+i}{i}$=$\frac{（1+i）（-i）}{-{i}^{2}}$=1-i，
∴$|z|=\sqrt{2}$，
故选：C．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，考查复数模的求法，是基础题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
如图，∠ACB=90°，DA⊥平面ABC，AE⊥DB交DB于E，AF⊥DC交DC于F，且AD=AB=2，则三棱锥D-AEF体积的最大值为$\frac{\sqrt{2}}{6}$．
18．若复数（m2-3m）+（m2-5m+6）i（m∈R））是纯虚数，则m的值为（ ）
| A． | 0 | B． | 2 | C． | 0或3 | D． | 2或3 |
2．
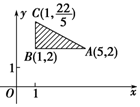如图所示的坐标平面的可行域内（包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）
如图所示的坐标平面的可行域内（包括边界），若使目标函数z=ax+y（a＞0）取得最大值的最优解有无穷多个，则a的值为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{3}{5}$ | C． | 4 | D． | $\frac{5}{3}$ |