题目内容
已知:函数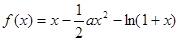 ,其中
,其中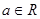 .
.
(Ⅰ)若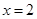 是
是 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在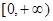 上的最大值是
上的最大值是 ,求
,求 的取值范围.
的取值范围.
(Ⅰ)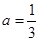
(Ⅱ)当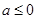 时,
时, 的增区间是
的增区间是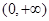 ,减区间是
,减区间是 ;
;
当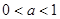 时,
时, 的增区间是
的增区间是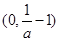 ,减区间是
,减区间是 和
和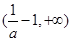 ;
;
当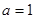 时,
时, 的减区间是
的减区间是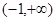 ;
;
当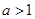 时,
时, 的增区间是
的增区间是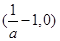 ;减区间是
;减区间是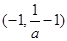 和
和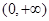 .
.
(Ⅲ)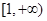
解析试题分析:(Ⅰ)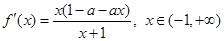 .
.
依题意,令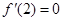 ,解得
,解得 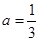 .
.
经检验,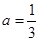 时,符合题意. ……4分
时,符合题意. ……4分
(Ⅱ)① 当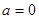 时,
时,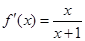 .
.
故 的单调增区间是
的单调增区间是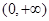 ;单调减区间是
;单调减区间是 . ……5分
. ……5分
② 当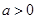 时,令
时,令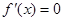 ,得
,得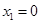 ,或
,或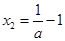 .
.
当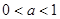 时,
时, 与
与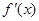 的情况如下:
的情况如下: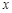
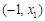
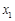
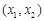
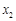
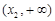
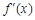
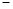

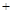

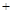
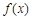
↘ 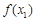
↗ 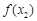
 练习册系列答案
练习册系列答案
夺冠金卷系列答案
期末考试金钥匙系列答案
45分钟课时作业与单元测试系列答案
必会必考精讲点练系列答案
步步高名校练考卷系列答案
系列答案
高中金牌单元测试系列答案
名师一号高中同步学习方略系列答案
华夏1卷通系列答案
课时方案新版新理念导学与测评系列答案
相关题目
 (a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切.
(a>0),g(x)=2lnx+bx且直线y=2x-2与曲线y=g(x)相切. )内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围;
)内的一切实数x,小等式f(x)≥g(x)恒成立,求实数a的取值范围; 成立;
成立; .
.
 时,求函数
时,求函数 的单调区间;
的单调区间; 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?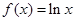 ,
,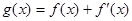 .
.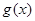 的单调区间和最小值;
的单调区间和最小值;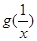 的大小关系;
的大小关系;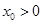 ,使得
,使得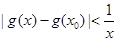 对任意
对任意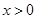 成立?若存在,求出
成立?若存在,求出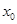 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.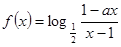 为奇函数,a为常数。
为奇函数,a为常数。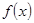 在区间
在区间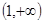 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。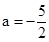 时,求函数f(x)的极小值.
时,求函数f(x)的极小值. ,
, 的单调区间;(II)求
的单调区间;(II)求 上的最小值。
上的最小值。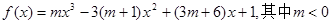 。
。 的单调增区间是(0,1)求m的值。
的单调增区间是(0,1)求m的值。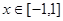 时,函数
时,函数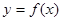 的图象上任意一点的切线斜率恒大于3m,求m的取值范围。
的图象上任意一点的切线斜率恒大于3m,求m的取值范围。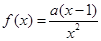 ,其中
,其中 .
.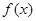 的单调区间;
的单调区间;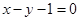 是曲线
是曲线 的切线,求实数
的切线,求实数 的值;
的值; ,求
,求 在区间
在区间 上的最大值.(其中
上的最大值.(其中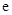 为自然对数的底数)
为自然对数的底数)