题目内容
12.对于函数y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$).(1)求该函数的周期;
(2)求该函数的最小值,并指出取得最小值时的x的集合;
(3)用五点法作出该函数在其一个周期上的图象.
分析 根据函数的解析式,利用正弦函数的周期性、最值得出结论,再利用五点法作函数在一个周期上的图象
解答 解:(1)对于函数y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$),它的周期为$\frac{2π}{\frac{1}{2}}$=4π.
(2)该函数的最小值为-$\frac{1}{2}$,此时,$\frac{1}{2}$x+$\frac{π}{4}$=2kπ-$\frac{π}{2}$,求得x=4kπ-$\frac{3π}{2}$,k∈Z,
故函数的最小值为-$\frac{1}{2}$,并指出取得最小值时的x的集合为{x|x=4kπ-$\frac{3π}{2}$,k∈Z}.
(3)列表:
| $\frac{1}{2}$x+$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{2}$ | $\frac{π}{2}$ | $\frac{3π}{2}$ | $\frac{5π}{2}$ | $\frac{7π}{2}$ |
| y | 0 | $\frac{1}{2}$ | 0 | -$\frac{1}{2}$ | 0 |
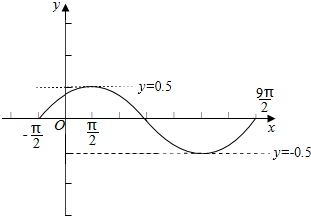
点评 本题主要考查正弦函数的周期性、最值,用五点法作函数的图象,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
7.已知实数a>0,函数f(x)的定义域为R,则“对任意的x∈R,都有f(x-a)=-f(x)”是“2a是函数f(x)的一个周期”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知tanx=-2,x在第四象限,则sinx=( )
| A. | -$\frac{2}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
1.已知sinθ=$\frac{3}{5}$,且$\frac{π}{2}$<θ<$\frac{3π}{2}$,则cos$\frac{θ}{2}$=( )
| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | ±$\frac{\sqrt{10}}{10}$ | D. | ±$\frac{3\sqrt{10}}{10}$ |
