题目内容
9.已知盒子中有4个红球,n个白球,若从中一次取出4个球,其中白球的个数为X,且E(X)=$\frac{12}{7}$.则n的值( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 X=0,1,2,3,4,则P(X=k)=$\frac{{∁}_{4}^{4-k}{∁}_{n}^{k}}{{∁}_{n+4}^{4}}$,(k=0,1,2,3,4).利用数学期望计算公式即可得出.
解答 解:X=0,1,2,3,4,
则P(X=k)=$\frac{{∁}_{4}^{4-k}{∁}_{n}^{k}}{{∁}_{n+4}^{4}}$,(k=0,1,2,3,4).
则P(X=0)=$\frac{1}{{∁}_{n+4}^{4}}$,P(X=1)=$\frac{4n}{{∁}_{n+4}^{4}}$,P(X=2)=$\frac{6{∁}_{n}^{2}}{{∁}_{n+4}^{4}}$,P(X=3)=$\frac{4{∁}_{n}^{3}}{{∁}_{n+4}^{4}}$,P(X=4)=$\frac{1}{{∁}_{n+4}^{4}}$,
∴E(X)=0+1×$\frac{4n}{{∁}_{n+4}^{4}}$+2×$\frac{6{∁}_{n}^{2}}{{∁}_{n+4}^{4}}$+3×$\frac{4{∁}_{n}^{3}}{{∁}_{n+4}^{4}}$+4×$\frac{1}{{∁}_{n+4}^{4}}$=$\frac{12}{7}$.
则n=3.
故选:A.
点评 本题考查了超几何分布列的概率计算公式及其数学期望、组合计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.一个半径为$\sqrt{6}$的球的内接正四棱柱的高为4,则该正四棱柱的表面积为( )
| A. | 24 | B. | 32 | C. | 36 | D. | 40 |
14.已知$\overrightarrow{a}$、$\overrightarrow{b}$均为单位向量,(2$\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=-$\frac{3\sqrt{3}}{2}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
1.已知角α的正弦线和余弦线长度相等,且α的终边在第三象限,则tanα等于( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\sqrt{3}$ |
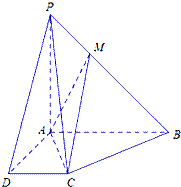 如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
如图所示,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.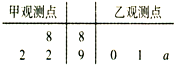 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.