题目内容
15.判断下列函数的奇偶性:①y=$\sqrt{cosx-1}$
②y=$\sqrt{\frac{1-x}{1+x}}$
③y=lg(x+$\sqrt{1+{x}^{2}}$)
分析 根据函数奇偶性的定义分别进行判断即可.
解答 解:①由cosx-1≥0得cosx=1,此时y=0,则函数f(x)既是奇函数又是偶函数.
②由$\frac{1-x}{1+x}$≥0得-1<x≤1,则函数的定义域关于原点不对称,则函数y=$\sqrt{\frac{1-x}{1+x}}$为非奇非偶函数.
③f(-x)+f(x)=lg(-x+$\sqrt{1+{x}^{2}}$)+lg(x+$\sqrt{1+{x}^{2}}$)=lg(-x+$\sqrt{1+{x}^{2}}$)(x+$\sqrt{1+{x}^{2}}$)=lg(1+x2-x2)=lg1=0,
则f(-x)=-f(x),即函数f(x)是奇函数.
点评 本题主要考查函数奇偶性的判断,根据函数奇偶性的定义,结合函数定义域的对称性是解决本题的关键.

练习册系列答案
相关题目
6.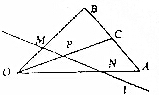 如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
 如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )
如图,在△AOB中,OC是边AB的中线,P是OC的中点,直线l与OB,OA分别交于点M,N,若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$,$\overrightarrow{OA}$=x$\overrightarrow{ON}$,则x=( )| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
3.已知数列{an}是等比数列且数列{|an|}是递增数列,a2+a3=2,a1a4=-8,则a2016=( )
| A. | $\frac{1}{{2}^{2015}}$ | B. | -$\frac{1}{{2}^{2015}}$ | C. | -22015 | D. | 22015 |