题目内容
8.已知圆C:(x-3)2+y2=4,直线l过点(2,0)与圆C交于两点A,B,则$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是( )| A. | [1,+∞) | B. | (-∞,5) | C. | [1,5] | D. | [1,5) |
分析 由题意画出图形,设出直线l的方程,联立直线方程与圆的方程,化为关于y的一元二次方程,利用根与系数的关系及数量积公式求解.
解答 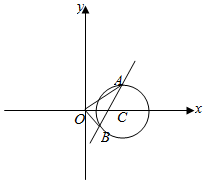 解:如图,
解:如图,
设直线l的方程为x=2+ty,
联立$\left\{\begin{array}{l}{x=2+ty}\\{(x-3)^{2}+{y}^{2}=4}\end{array}\right.$,得(t2+1)y2-2ty-3=0.
设A(x1,y1),B(x2,y2),
则${y}_{1}+{y}_{2}=\frac{2t}{{t}^{2}+1}$,${y}_{1}{y}_{2}=-\frac{3}{{t}^{2}+1}$.
x1x2=(ty1+2)(ty2+2)=t2y1y2+2t(y1+y2)+4
=$\frac{-3{t}^{2}}{{t}^{2}+1}+\frac{4{t}^{2}}{{t}^{2}+1}+4=\frac{5{t}^{2}+4}{{t}^{2}+1}$.
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=$\frac{5{t}^{2}+4}{{t}^{2}+1}-\frac{3}{{t}^{2}+1}=\frac{5{t}^{2}+1}{{t}^{2}+1}=5-\frac{4}{{t}^{2}+1}$.
∵t2+1≥1,1≤$5-\frac{4}{{t}^{2}+1}<5$.
∴$\overrightarrow{OA}•\overrightarrow{OB}$的取值范围是[1,5).
故选:D.
点评 本题考查平面向量的数量积运算,考查数形结合的解题思想方法与数学转化思想方法,是中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
18.若将函数y=sin2x的图象向右平移$\frac{π}{12}$个单位长度,则平移后的图象的对称轴方程为( )
| A. | x=$\frac{kπ}{2}$$-\frac{7π}{12}$(k∈Z) | B. | x=$\frac{kπ}{2}$$+\frac{7π}{12}$(k∈Z) | C. | x=$\frac{kπ}{2}$$-\frac{π}{3}$(k∈Z) | D. | x=$\frac{kπ}{2}$$+\frac{π}{3}$(k∈Z) |
16.函数f(x)=log2(x-1)+log2(3-x)( )
| A. | 在(1,3)上是增函数 | B. | 在(1,3)上是减函数 | C. | 最小值为1 | D. | 最大值为0 |
13.我市在对高三学生的综合素质评价中,将其测评结果分为“A、B、C”三个等级,其中A表示“优秀”,B表示“良好”,C表示“合格”.
(1)某校高三年级有男生1000人,女生700人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高三学生中抽取了85名学生的综合素质评价结果,其各个等级的频数统计如表:
根据表中统计的数据填写下面2×2列联表,并判断是否有95%的把握认为“综合素质评价测评结果为优秀与性别有关”?
(2)以(1)中抽取的85名学生的综合素质评价等级为“合格”的学生中按分层抽样随机抽取6人.再从这6人中任选2人去参加“提高班”培训,求所选6人中恰有2人为男生的概率.
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
临界值表:
(1)某校高三年级有男生1000人,女生700人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高三学生中抽取了85名学生的综合素质评价结果,其各个等级的频数统计如表:
| 等级 | 优秀 | 良好 | 合格 |
| 男生(人) | 16 | x | 8 |
| 女生(人) | 18 | 13 | y |
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
临界值表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
17.在函数y=2x,y=x2,y=2x,y=cosx中,偶函数的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.函数y=x2-x3的单调增区间为( )
| A. | (0,+∞) | B. | (0,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,+∞) | D. | (1,+∞) |