题目内容
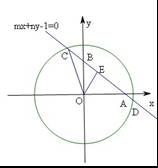
设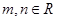 ,若直线
,若直线 与
与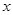 轴相交于点
轴相交于点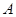 ,与
,与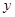 轴相交于
轴相交于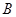 ,且
,且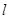 与圆
与圆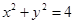 相交所得弦的长为2,
相交所得弦的长为2,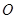 为坐标原点,则
为坐标原点,则 面积的最小值为_________.
面积的最小值为_________.
【答案】
3
【解析】
试题分析:直线与两坐标轴的交点坐标为 ,
,
直线与圆相交所得的弦长为2,圆心到直线的距离 满足
满足 ,
,
所以 ,即圆心到直线的距离
,即圆心到直线的距离 ,
,
所以 .
.
三角形的面积为 ,又
,又 ,
,
当且仅当 时取等号,所以最小值为
时取等号,所以最小值为 .
.
考点:本小题主要考查直线与圆的位置关系、三角形面积公式和基本不等式的应用,考查学生综合运用所学知识解决问题的能力和运算求解能力.
点评:解决直线与圆的位置关系的题目时,一般用几何法可以简化运算;用基本不等式时,一定要注意“一正二定三相等”三个条件缺一不可,而且还要交代清楚取等号的条件.

练习册系列答案
相关题目
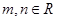 ,若直线
,若直线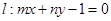 与
与 轴相交于点
轴相交于点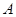 ,与
,与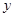 轴相交于
轴相交于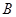 ,且
,且 与圆
与圆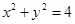 相交所得弦的长为2,
相交所得弦的长为2, 为坐标原点,求
为坐标原点,求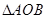 面积的最小值.
面积的最小值.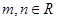 ,若直线
,若直线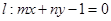 与
与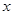 轴相交于点
轴相交于点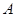 ,与
,与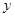 轴相交于点
轴相交于点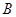 ,且坐标原点
,且坐标原点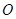 到
到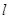 的距离为
的距离为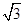 ,则
,则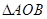 面积的最小值为( )
面积的最小值为( )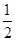 B.
B.
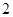 C.
C.
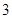 D.
D.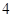
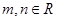 ,若直线
,若直线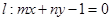 与
与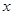 轴相交于点A,与y轴相交于B,且l与圆
轴相交于点A,与y轴相交于B,且l与圆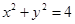 相交所得弦的长为2,O为坐标原点,则
相交所得弦的长为2,O为坐标原点,则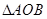 面积的最小值为 。
面积的最小值为 。