题目内容
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
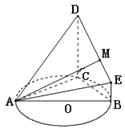
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
【答案】(1)答案详见解析;(2)存在,且![]() .
.
【解析】
试题(1)由已知中CD⊥⊙O所在的平面,BE∥CD,易得BE⊥平面ABC,则BE⊥AB,由BE=1,![]() ,易得AB是⊙O的直径,则AC⊥BC由线面垂直的判定定理可得CD⊥平面ABC,再由面面垂直的判定定理可得平面ADC⊥平面BCDE;(2)方法一:过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF,可得∠MAN为MA与平面ACD所成的角,设MN=x,则由直线AM与平面ACD所成角的正弦值为
,易得AB是⊙O的直径,则AC⊥BC由线面垂直的判定定理可得CD⊥平面ABC,再由面面垂直的判定定理可得平面ADC⊥平面BCDE;(2)方法一:过点M作MN⊥CD于N,连接AN,作MF⊥CB于F,连接AF,可得∠MAN为MA与平面ACD所成的角,设MN=x,则由直线AM与平面ACD所成角的正弦值为![]() ,我们可以构造关于x的方程,解方程即可求出x值,进而得到点M的位置.方法二:建立如图所示空间直角坐标系C-xyz,求出平面ABC的法向量和直线AM的方向向量(含参数λ),由直线AM与平面ACD所成角的正弦值为
,我们可以构造关于x的方程,解方程即可求出x值,进而得到点M的位置.方法二:建立如图所示空间直角坐标系C-xyz,求出平面ABC的法向量和直线AM的方向向量(含参数λ),由直线AM与平面ACD所成角的正弦值为![]() ,根据向量夹角公式,我们可以构造关于λ的方程,解方程即可得到λ值,进而得到点M的位置.
,根据向量夹角公式,我们可以构造关于λ的方程,解方程即可得到λ值,进而得到点M的位置.
试题解析:(1)∵CD ⊥平面ABC,BE//CD
∴BE⊥平面ABC,∴BE⊥AB
∵BE=1,![]() ∴
∴![]() ,
,
从而![]()
∵⊙![]() 的半径为
的半径为![]() ,∴AB是直径,
,∴AB是直径,
∴AC⊥BC
又∵CD ⊥平面ABC,∴CD⊥BC,故BC⊥平面ACD
![]() 平面BCDE,∴平面ADC
平面BCDE,∴平面ADC![]() 平面BCDE
平面BCDE
(2)方法1:
假设点M存在,过点M作MN⊥CD于N,连结AN,作MF⊥CB于F,连结AF
∵平面ADC![]() 平面BCDE,
平面BCDE,
∴MN⊥平面ACD,∴∠MAN为MA与平面ACD所成的角
设MN=x,计算易得,DN=![]() ,MF=
,MF=![]()
故![]()
![]() 解得:
解得:![]() (舍去)
(舍去)![]() ,…11分
,…11分
故![]() ,从而满足条件的点
,从而满足条件的点![]() 存在,且
存在,且![]()
方法2:建立如图所示空间直角坐标系C—xyz,
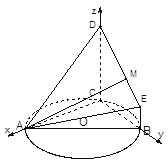
则:A(4,0,0),B(0,2,0),D(0,0,4),E(0,2,1),O(0,0,0),则![]()
易知平面ABC的法向量为![]() ,假设M点存在,设
,假设M点存在,设![]() ,则
,则![]() ,再设
,再设![]()
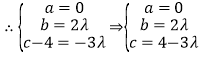 ,
,
即![]() ,从而
,从而![]() …10分
…10分
设直线BM与平面ABD所成的角为![]() ,则:
,则:
![]()
解得![]() ,其中
,其中![]() 应舍去,而
应舍去,而![]() 故满足条件的点M存在,且点M的坐标为
故满足条件的点M存在,且点M的坐标为![]()

【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
分数段 |
|
|
|
|
| 1∶1 | 2∶1 | 3∶4 | 4∶5 |

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.