题目内容
【题目】在四棱柱ABCD－A1B1C1D1中，
,平面BB1C1C
底面ABCD，点
、F分别是线段
、BC的中点．
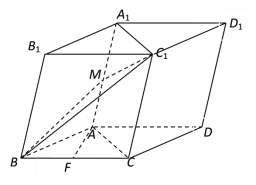
（1）求证：AF//平面
；
（2）求证：平面BB1C1C⊥平面．
【答案】（1）见解析； （2）见解析.
【解析】
（1）欲证AF//平面
，则需证明
平行于平面内的一条直线，根据题目条件易得
边上的中线与平行，从而得证。
（2）需证面面垂直，则需证明线面垂直，易证边上的中线垂直于且，该中线垂直于
，从而得到线面垂直，得到面面垂直。
（1）方法一：取中点
，连
分别为
中点
为四棱柱
又
为
的中点，
所以四边形PFAM为平行四边形
又
，
方法二：取
中点
,连
，
又
，
，
又是四棱柱，
，
，
，
，
，
又
，
，又
，又
，
（2）
，
，
又
,
，
，
又
，
，
而
， 
又
，
， 又
.
练习册系列答案
相关题目
