题目内容
定义数列如下:a1=2,an+1=an2-an+1,n∈N*.证明:
(Ⅰ)对于n∈N*,恒有an>1成立;
(Ⅱ)当n>2且n∈N*,有an+1=anan-1…a2a1+1成立;
(Ⅲ)1-
<
+
+…+
<1.
(Ⅰ)对于n∈N*,恒有an>1成立;
(Ⅱ)当n>2且n∈N*,有an+1=anan-1…a2a1+1成立;
(Ⅲ)1-
| 1 |
| 22014 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
考点:数列的求和,数列的函数特性
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)利用数学归纳法、二次函数的性质进行证明结论成立;
(Ⅱ)由an+1=an2-an+1得an+1-1=an(an-1),即当n≥2时,an-1=an-1(an-1),再给n=2、3、…、n列出式子,由迭代法进行证明结论成立;
(Ⅲ)由
得
=
-
,利用裂项相消法
+
+…+
化简后可证明右边,由题意得an+1-an=an2-an+1-an=(an-1)2>0,判断出数列是递增数列,由(Ⅱ)的结论化简,再进行适当的放缩可证明左边.
(Ⅱ)由an+1=an2-an+1得an+1-1=an(an-1),即当n≥2时,an-1=an-1(an-1),再给n=2、3、…、n列出式子,由迭代法进行证明结论成立;
(Ⅲ)由
|
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
解答:
证明:(Ⅰ)当n=1时,a1=2>1成立,
当k≥2时,假设ak>1成立,
那么当n=k+1时,因为ak+1=ak2-ak+1=(ak-
)2+
在(1,+∞)递增,
所以ak+1>1也成立,
综上得,对于n∈N*,恒有an>1成立;
(Ⅱ)由an+1=an2-an+1得,an+1-1=an(an-1),
∴当n≥2时,an-1=an-1(an-1),
则a2-1=a1(a1-1),a3-1=a2(a2-1),…,
an+1-1=an(an-1),
由以上各式迭代得,an+1-1=anan-1…a2a1(a1-1),
∵a1=2,∴an+1=anan-1…a2a1+1;
(Ⅲ)∵an+1=an2-an+1,且a1=2,
∴an+1-an=an2-an+1-an=(an-1)2>0,
即an+1>an,则数列{an}是单调递增数列,
∵
,∴
=
-
,
∴
=
-
,
∴
+
+…+
=(
-
)+(
-
)+…+(
-
)
=
-
=1-
<1,
由(Ⅱ)得,an+1=anan-1…a2a1+1,
∴a2015-1=a2014a2013…a2a1,
∴1-
=1-
,
∵数列{an}是单调递增数列,且a1=2,
∴1-
>1-
=1-
,
综上得,1-
<
+
+…+
<1,原不等式得证.
当k≥2时,假设ak>1成立,
那么当n=k+1时,因为ak+1=ak2-ak+1=(ak-
| 1 |
| 2 |
| 3 |
| 4 |
所以ak+1>1也成立,
综上得,对于n∈N*,恒有an>1成立;
(Ⅱ)由an+1=an2-an+1得,an+1-1=an(an-1),
∴当n≥2时,an-1=an-1(an-1),
则a2-1=a1(a1-1),a3-1=a2(a2-1),…,
an+1-1=an(an-1),
由以上各式迭代得,an+1-1=anan-1…a2a1(a1-1),
∵a1=2,∴an+1=anan-1…a2a1+1;
(Ⅲ)∵an+1=an2-an+1,且a1=2,
∴an+1-an=an2-an+1-an=(an-1)2>0,
即an+1>an,则数列{an}是单调递增数列,
∵
|
| 1 |
| an+1-1 |
| 1 |
| an-1 |
| 1 |
| an |
∴
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| an+1-1 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
| 1 |
| a1-1 |
| 1 |
| a2-1 |
| 1 |
| a2-1 |
| 1 |
| a3-1 |
| 1 |
| a2014-1 |
| 1 |
| a2015-1 |
=
| 1 |
| a1-1 |
| 1 |
| an+1-1 |
| 1 |
| a2015-1 |
由(Ⅱ)得,an+1=anan-1…a2a1+1,
∴a2015-1=a2014a2013…a2a1,
∴1-
| 1 |
| a2015-1 |
| 1 |
| a1a2…a2014 |
∵数列{an}是单调递增数列,且a1=2,
∴1-
| 1 |
| a1a2…a2014 |
| 1 |
| a1a1…a1 |
| 1 |
| 22014 |
综上得,1-
| 1 |
| 22014 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
点评:本题考查数学归纳法,迭代法,裂项相消法求数列的和,利用作差法:an+1-an,判断出数列的单调性,以及利用放缩法证明不等式,综合性强,难度大,考查了较强的逻辑推理能力.

练习册系列答案
相关题目
向量
=(-3,4),
=(-8,-6),则
,
关系为( )
| a |
| b |
| a |
| b |
| A、垂直 | B、同向平行 |
| C、反向平行 | D、共线 |
命题“?x∈R,x2+2x+2≤0”的否定是( )
| A、?x∈R,x2+2x+2>0 |
| B、?x∈R,x2+2x+2≤0 |
| C、?x∈R,x2+2x+2>0 |
| D、?x∈R,x2+2x+2≥0 |
设a=log
3,b=(
)0.3,c=lnπ,则( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、c<a<b |
| B、a<c<b |
| C、a<b<c |
| D、b<a<c |
已知全集U={1,2,3,4,5},A={1,3,5},则∁UA=( )
| A、{1,2} |
| B、{2,4,5} |
| C、{2,3,4} |
| D、{2,4} |
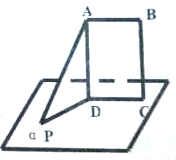 如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.
如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.