题目内容
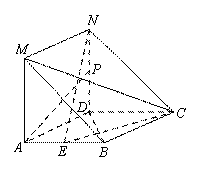
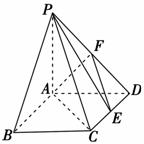
在如图所示的几何体中,四边形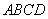 是菱形,
是菱形,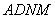 是矩形,平面
是矩形,平面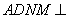 平面
平面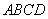 ,
,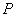 为
为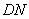 的中点.
的中点.
(1)求证: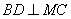 ;
;
(2)在线段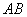 上是否存在点
上是否存在点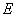 ,使得
,使得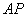 ∥平面
∥平面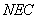 ,
,
若存在,说明其位置,并加以证明;若不存在,请说明理由.
 |
 【解析】(1)证明:连结
【解析】(1)证明:连结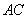 ,
,
∵四边形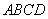 是菱形,∴
是菱形,∴ ,
,
∵四边形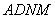 是矩形,∴
是矩形,∴ ,
,
∵平面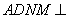 平面
平面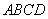 ,
,
平面 平面
平面 ,
,
 平面
平面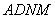 ,∴
,∴ 平面
平面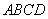 ,
,
∵ 平面
平面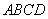 ,∴
,∴ ,∵
,∵ ,∴
,∴ 平面
平面 ,
,
∵ 平面
平面 ,∴
,∴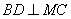 .
.
(2)当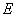 为
为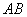 的中点时,有
的中点时,有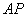 //平面
//平面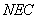 .
.
证明:取 的中点
的中点 ,连结
,连结 ,
, .
.
∵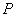 为
为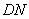 的中点,
的中点, 是
是 的中点,∴
的中点,∴ //
// ,且
,且 ,
,
∵ //
// ,且
,且 ,∴
,∴ //
// ,且
,且 ,
,
∴四边形 为平行四边形,∴
为平行四边形,∴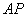 //
// ,
,
∵ 平面
平面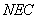 ,
, 平面
平面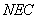 ,∴
,∴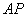 //平面
//平面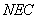 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 B.
B. C.
C. D.
D.

 中,
中, .
. 平面
平面

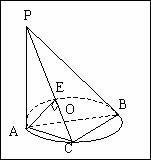
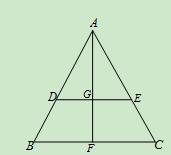
 的等边三角形
的等边三角形 中,
中,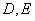 分别是
分别是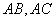 边上的点,
边上的点,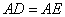 ,
,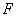 是
是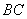 的中点,
的中点,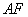 与
与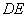 交于点
交于点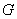 ,将
,将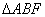 沿
沿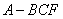 ,其中
,其中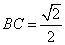 .
.
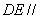 平面
平面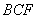 ;(2) 证明:
;(2) 证明: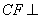 平面
平面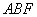 ;
;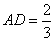 时,求三棱锥
时,求三棱锥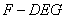 的体积
的体积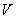 .
. 中,
中,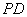 垂直于底面
垂直于底面 ,底面
,底面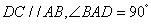 ,且
,且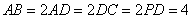 (单位:
(单位: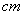 ),
),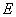 为
为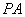 的中点。
的中点。
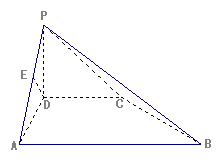 (1)如图,若正视方向与
(1)如图,若正视方向与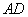 平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积;
平行,请在下面(答题区)方框内作出该几何体的正视图并求出正视图面积; 平面
平面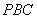 ;
;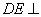 平面
平面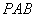 ;
; .若存在
.若存在 的极值点
的极值点 满足
满足 ,则m的取值范围是( )
,则m的取值范围是( ) B.
B.
 D.
D.
 ,
, 的最大值是( )
的最大值是( ) .
.
 B.-1
B.-1  .0
.0  .1
.1