题目内容
如图,A,B,C是椭圆M: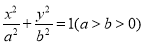 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
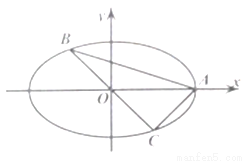
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
(1)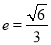 (2)
(2)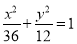
【解析】
试题分析:(1)有条件列出C点坐标是解题关键:因为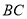 过椭圆
过椭圆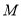 的中心,所以
的中心,所以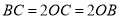 ,又
,又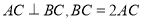 ,所以
,所以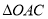 是以角
是以角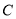 为直角的等腰直角三角形,则
为直角的等腰直角三角形,则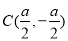 所以
所以 ,则
,则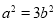 ,
,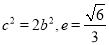 (2)本题关键为表示出△ABC的外接圆方程:
(2)本题关键为表示出△ABC的外接圆方程: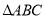 的外接圆直径为AB,所以易得
的外接圆直径为AB,所以易得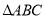 的外接圆为:
的外接圆为: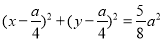 ,由垂径定理得
,由垂径定理得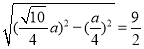 即
即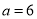 ,所以椭圆方程为
,所以椭圆方程为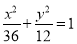 .
.
试题解析:(1)因为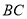 过椭圆
过椭圆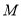 的中心,所以
的中心,所以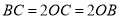 ,
,
又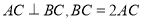 ,所以
,所以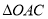 是以角
是以角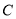 为直角的等腰直角三角形, 3分
为直角的等腰直角三角形, 3分
则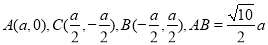 ,所以
,所以 ,则
,则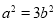 ,
,
所以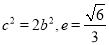 ; 7分
; 7分
(2)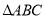 的外接圆圆心为
的外接圆圆心为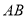 中点
中点 ,半径为
,半径为 ,
,
则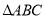 的外接圆为:
的外接圆为: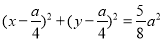 10分
10分
令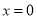 ,
,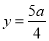 或
或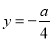 ,所以
,所以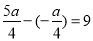 ,得
,得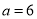 ,
,
(也可以由垂径定理得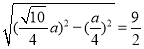 得
得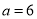 )
)
所以所求的椭圆方程为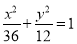 . 15分
. 15分
考点:椭圆方程,椭圆离心率
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 的定义域为()
的定义域为() 
 如下:
如下: ,且当
,且当 时,
时, ,其中
,其中 是不同的质数.
是不同的质数. 为12的全部不同正因数的集合,则
为12的全部不同正因数的集合,则 .
.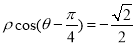 ,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,曲线C2的参数方程为
,以极点为原点,极轴为x轴的非负半轴建立平面直角坐标系,曲线C2的参数方程为 ,求曲线C1与曲线C2交点的直角坐标
,求曲线C1与曲线C2交点的直角坐标


 中,
中, ,
, ,则数列的前
,则数列的前 项和为 .
项和为 .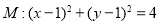 ,直线
,直线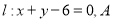 为直线
为直线 上一点,若圆
上一点,若圆 上存在两点
上存在两点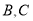 ,使得
,使得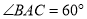 ,则点A的横坐标的取值范围是 .
,则点A的横坐标的取值范围是 .