题目内容
已知圆C:(x-2)2+(y-3)2=25,点P(-1,7),过点P作圆的切线,则该切线的一般式方程为 .
考点:圆的切线方程
专题:计算题,直线与圆
分析:由题意得圆C:(x-2)2+(y-3)2=25的圆心为C(2,3),半径r=5.P在圆上,可设切线l的方程,根据直线l与圆相切,利用点到直线的距离公式建立关于k的等式,解出k,即可得所求切线方程.
解答:
解:圆C:(x-2)2+(y-3)2=25的圆心为C(2,3),半径r=5.P在圆上.
由题意,设方程为y-7=k(x+1),即kx-y+7+k=0.
∵直线l与圆C:(x-2)2+(y-3)2=25相切,
∴圆心到直线l的距离等于半径,即d=
=5,解之得k=
,
因此直线l的方程为y-7=
(x+1),化简得3x-4y+31=0.
故答案为:3x-4y+31=0.
由题意,设方程为y-7=k(x+1),即kx-y+7+k=0.
∵直线l与圆C:(x-2)2+(y-3)2=25相切,
∴圆心到直线l的距离等于半径,即d=
| |2k-3+7+k| | ||
|
| 3 |
| 4 |
因此直线l的方程为y-7=
| 3 |
| 4 |
故答案为:3x-4y+31=0.
点评:本题给出圆的方程,求圆经过定点的切线方程.着重考查了点到直线的距离公式、圆的标准方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )


| A、(l,+∞) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-3)∪(-1,1) |
棱长为2的正方体的外接球的表面积为( )
| A、4π | B、12π |
| C、24π | D、48π |
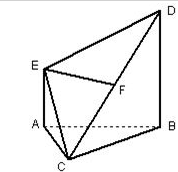 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.