题目内容
18.已知函数f(x)=$\sqrt{3}$cos(2x-$\frac{π}{3}$)-2sinxcosx.(I)求f(x)的最小正周期;
(II)求证:当x∈[-$\frac{π}{4}$,$\frac{π}{4}$]时,f(x)≥-$\frac{1}{2}$.
分析 (Ⅰ)根据两角差的余弦公式和两角和正弦公式即可求出f(x)sin(2x+$\frac{π}{3}$),根据周期的定义即可求出,
(Ⅱ)根据正弦函数的图象和性质即可证明.
解答 解:(Ⅰ)f(x)=$\sqrt{3}$cos(2x-$\frac{π}{3}$)-2sinxcosx,
=$\sqrt{3}$($\frac{1}{2}$co2x+$\frac{\sqrt{3}}{2}$sin2x)-sin2x,
=$\frac{\sqrt{3}}{2}$cos2x+$\frac{1}{2}$sin2x,
=sin(2x+$\frac{π}{3}$),
∴T=$\frac{2π}{2}$=π,
∴f(x)的最小正周期为π,
(Ⅱ)∵x∈[-$\frac{π}{4}$,$\frac{π}{4}$],
∴2x+$\frac{π}{3}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴-$\frac{1}{2}$≤sin(2x+$\frac{π}{3}$)≤1,
∴f(x)≥-$\frac{1}{2}$
点评 本题考查了三角函数的化简以及周期的定义和正弦函数的图象和性质,属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
13.根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080,则下列各数中与$\frac{M}{N}$最接近的是( )
(参考数据:lg3≈0.48)
(参考数据:lg3≈0.48)
| A. | 1033 | B. | 1053 | C. | 1073 | D. | 1093 |
3.函数f(x)=$\frac{1}{5}$sin(x+$\frac{π}{3}$)+cos(x-$\frac{π}{6}$)的最大值为( )
| A. | $\frac{6}{5}$ | B. | 1 | C. | $\frac{3}{5}$ | D. | $\frac{1}{5}$ |
7.若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点,则f(x)的极小值为( )
| A. | -1 | B. | -2e-3 | C. | 5e-3 | D. | 1 |
 如图,已知抛物线x2=y,点A(-$\frac{1}{2}$,$\frac{1}{4}$),B($\frac{3}{2}$,$\frac{9}{4}$),抛物线上的点P(x,y)(-$\frac{1}{2}$<x<$\frac{3}{2}$),过点B作直线AP的垂线,垂足为Q.
如图,已知抛物线x2=y,点A(-$\frac{1}{2}$,$\frac{1}{4}$),B($\frac{3}{2}$,$\frac{9}{4}$),抛物线上的点P(x,y)(-$\frac{1}{2}$<x<$\frac{3}{2}$),过点B作直线AP的垂线,垂足为Q.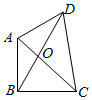 如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )
如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,则( )