题目内容
化简与求值:
(1)(2a
b
)(-6a
b
)÷(-3a
b
);
(2)(lg2)2+lg2•lg5+
.
(1)(2a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
(2)(lg2)2+lg2•lg5+
| (lg2)2-2lg2+1 |
考点:对数的运算性质,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:根据指数幂和对数的基本运算即可得到结论.
解答:
解:(1)(2a
b
)(-6a
b
)÷(-3a
b
)
=4a
+
-
•b
+
-
=4a.
2)(lg2)2+lg2•lg5+
=(lg2)2+lg2•lg5+1-lg2
=lg2(1g2+lg5)+1-lg2
=lg2+1-lg2=1.
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
=4a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
2)(lg2)2+lg2•lg5+
| (lg2)2-2lg2+1 |
=(lg2)2+lg2•lg5+1-lg2
=lg2(1g2+lg5)+1-lg2
=lg2+1-lg2=1.
点评:本题主要考查指数幂和对数的基本运算,根据相应的运算法则是解决本题的关键,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若复数z=
(其中i是虚数单位),则|z|=( )
| ||
| 1+i |
A、2
| ||
B、
| ||
| C、1 | ||
| D、1 |
已知命题p:函数y=
的定义域是(-∞,-3]∪[1,+∞);命题q:若a,b∈R,则|a+b|<1是|a|+|b|<1的充分而不必要条件,则下列命题中为真命题的是( )
| |x+1|-2 |
| A、p∧q |
| B、(¬p)∨q |
| C、p∨(¬q) |
| D、(¬p)∧(¬q) |
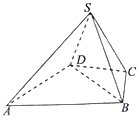 已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,
已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,