题目内容
2.阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=B 有α=$\frac{A+B}{2}$,β=$\frac{A-B}{2}$
代入③得 sinA+sinB=2sin$\frac{A+B}{2}$cos$\frac{A-B}{2}$.
类比上述推证方法,根据两角和与差的余弦公式,证明:
cosA-cosB=-2sin$\frac{A+B}{2}$sin$\frac{A-B}{2}$.
分析 通过两角和与差的余弦公式,令α+β=A,α-β=B有α=$\frac{A+B}{2}$,β=$\frac{A-B}{2}$,即可证明结果.
解答 证明:因为cos(α+β)=cosαcosβ-sinαsinβ,------①
cos(α-β)=cosαcosβ+sinαsinβ②
①-②得cos(α+β)-cos(α-β)=-2sinαsinβ③…
令α+β=A,α-β=B有α=$\frac{A+B}{2}$,β=$\frac{A-B}{2}$,
代入③得cosA-cosB=-2sin $\frac{A+B}{2}$sin$\frac{A-B}{2}$.
点评 本小题主要考查类比推理,考查两角和与差三角函数公式、二倍角公式、三角函数的恒等变换等基础知识,考查推理论证能力,运算求解能力,考查化归与转化思想等.

练习册系列答案
相关题目
12.同时投掷3枚硬币,那么互为对立事件的是( )
| A. | 至少有一个正面和最多一个正面 | B. | 最多两个正面和至少两个正面 | ||
| C. | 不多于一个正面和至少两个正面 | D. | 至少两个正面和恰有一个正面 |
17.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面A的图形的序号是( )
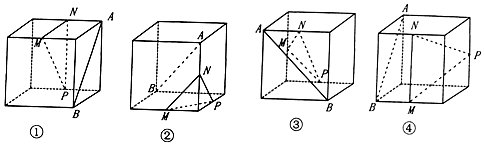

| A. | ①② | B. | ②③ | C. | ①③ | D. | ①③④ |
14.双曲线C的左,右焦点分别为F1(-1,0),F2(1,0),抛物线y2=4x与双曲线C的一个交点为P,若($\overrightarrow{{F}_{2}P}$+$\overrightarrow{{F}_{2}{F}_{1}}$)•($\overrightarrow{{F}_{2}P}$-$\overrightarrow{{F}_{2}{F}_{1}}$)=0,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | 1+$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
11.已知复数z满足1+i=(1-i)2z,则z的共轭复数在复平面内所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.圆ρ=r与圆ρ=-2rsin(θ+$\frac{π}{4}$)(r>0)的公共弦所在直线的方程为( )
| A. | 2ρ(sin θ+cos θ)=r | B. | 2ρ(sin θ+cos θ)=-r | ||
| C. | $\sqrt{2}$ρ(sin θ+cos θ)=r | D. | $\sqrt{2}$ρ(sin θ+cos θ)=-r |
