题目内容
1.已知某几何体的三视图如图所示(单位:cm),则其体积是$\frac{5}{6}$.
分析 几何体为直三棱柱切去一个小三棱锥.
解答 解:几何体为直三棱柱切去一个三棱锥得到的.三棱柱底面为左视图中三角形,棱柱的高为2,
切去的三棱锥的底面与三棱柱的底面相同,高为1,
所以几何体的体积V=$\frac{1}{2}×1×1×2$-$\frac{1}{3}×\frac{1}{2}×1×1×1$=$\frac{5}{6}$.
故答案为$\frac{5}{6}$.
点评 本题考查了空间几何体的三视图,结构特征和体积计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.给出下列命题:
①若a,b,m都是正数,且$\frac{a+m}{b+m}>\frac{a}{b}$,则a<b;
②若f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,x2-2x+1<0”的否定是真命题;
④“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件.
其中正确命题的序号是( )
①若a,b,m都是正数,且$\frac{a+m}{b+m}>\frac{a}{b}$,则a<b;
②若f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,x2-2x+1<0”的否定是真命题;
④“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件.
其中正确命题的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
9.设a=30.5,b=log32,c=cos$\frac{2π}{3}$,则( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
16.设平面向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,则“$\overrightarrow{a}$=$\overrightarrow{b}$”是“($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$=0”的( )
| A. | 充分不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.设$a={π^{0.3}},b={log_π}3,c={log_3}sin\frac{2π}{3}$,则( )
| A. | a>b>c | B. | c>a>b | C. | b>a>c | D. | b>c>a |
10.若z(1+i)=(1-i)2(i为虚数单位),则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
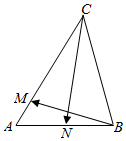 在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.
在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.