题目内容
2.函数f(x)=$\frac{sin2x}{cosx}$的最小正周期是2π.分析 由三角函数公式化简可得f(x)=2sinx,由周期公式可得
解答 解:f(x)=$\frac{sin2x}{cosx}$=$\frac{2sinxcosx}{cosx}$=2sinx,
∴f(x)的最小正周期T=$\frac{2π}{1}$=2π,
故答案为:2π
点评 本题考查三角函数恒等变换,涉及二倍角公式和三角函数的周期,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知a=2-sin1,b=-$\frac{π}{6}$+sin$\frac{π}{12}$,c=-$\frac{π}{4}$+sin$\frac{π}{8}$,则( )
| A. | b>c>a | B. | a>b>c | C. | a>c>b | D. | b>a>c |
11.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点F与抛物线y2=2px(p>0)的焦点重合,且在第一象限的交点为M,MF直于x轴,则双曲线的离心率是( )
| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\sqrt{2}$+2 |
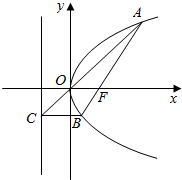 过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.
过抛物线y2=2px的焦点F的直线和抛物线相交于A,B两点,如图所示.