题目内容
 如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则AC1=
如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则AC1=考点:棱柱的结构特征
专题:空间位置关系与距离
分析:观察图形及题设条件,可构造出与AC1有关的三角形然后利用三角形求此线段的长度,由题设条件可以证出AA1在底面上的射影是角BAD的角平分线,由几何体的几何特征知,CC1在底面上的射影在BC,DC的所组成的角的角平分线上,且此垂足到C的距离与点A1在底面的垂足O到A的距离相,故可依据题设条件求出点O到AB,AD的距离,即求得图中HR,CR的长度,补出如图的图形,在直角三角形中即可求出AC1的长.
解答:
解:由题意,如图,作A1O⊥底面于O,作OE垂直AB于E,OF垂直AD于F,连接A1F,A1E,
由于,∠BAA1=∠DAA1=60°,故有△A1FA≌△A1EA,即A1F=A1E
从而有△A1FO≌△A1EO,即有OF=OE,由作图知,O在角DAB的角平分线上,
又底面是矩形,故角DAO=角BAO=45°,
又AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,
∴A1F=A1E=5
,AE=AF=
,于是有AO=
,
在直角三角形A1OA中,解得A1O=
,
在图中作C1H垂直底面于H,作HR垂直DC延长线与R,由几何体的性质知,HR=CR=
,A1O=C1H=
,
连接AH,得如图的直角三角形ASH,直角三角形AHC1,由已知及上求解得AS=
,SH=
∴AC12=AH2+C1H2=AS2+SH2+C1H2=
+
+
=85,
∴AC1=
,
故答案为:
由于,∠BAA1=∠DAA1=60°,故有△A1FA≌△A1EA,即A1F=A1E

从而有△A1FO≌△A1EO,即有OF=OE,由作图知,O在角DAB的角平分线上,
又底面是矩形,故角DAO=角BAO=45°,
又AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,
∴A1F=A1E=5
| 3 |
| 5 |
| 2 |
5
| ||
| 2 |
在直角三角形A1OA中,解得A1O=
5
| ||
| 2 |
在图中作C1H垂直底面于H,作HR垂直DC延长线与R,由几何体的性质知,HR=CR=
| 5 |
| 2 |
5
| ||
| 2 |
连接AH,得如图的直角三角形ASH,直角三角形AHC1,由已知及上求解得AS=
| 13 |
| 2 |
| 11 |
| 2 |
∴AC12=AH2+C1H2=AS2+SH2+C1H2=
| 169 |
| 4 |
| 121 |
| 4 |
| 50 |
| 4 |
∴AC1=
| 85 |
故答案为:
| 85 |
点评:本题主要考查了体对角线的求解,同时考查了空间想象能力,计算推理的能力,本题解题的关键是有着较强的空间感知能力以及根据题设条件构造图形的能力,本题是一个创造型题,作出恰当的辅助线对求解本题很重要,本题是立体几何中综合性较强的题,解题中用到了间接法的技巧,通过求点A1到底面的距离求出点C1到底面的距离.

练习册系列答案
相关题目
复数
的共轭复数是( )
| i |
| 1-i |
A、-
| ||||||
B、-
| ||||||
C、-
| ||||||
D、
|
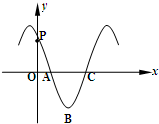 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.