题目内容
10．已知动直线kx-y+4-3k=0与圆x2+y2-6x-8y+24=0交于A，B两点，平面上的动点P满足：|$\overrightarrow{PA}$+$\overrightarrow{PB}$|=4，则动点P到坐标原点O的距离的最大值为多少．分析 由条件可得直线经过圆心，点P在以点M为圆心、半径等于2的圆上，求得OM的值，则OM+2为所求．
解答 解：动直线kx-y+4-3k=0，即 k（x-3）-y+4=0，经过定点M（3，4），
圆x2+y2-6x-8y+24=0，即 （x-3）2+（y-4）2=1，表示以M（3，4）为圆心、半径等于1的圆．
故线段AB的中点为M，故有$\overrightarrow{PA}$+$\overrightarrow{PB}$=2$\overrightarrow{PM}$．
结合|$\overrightarrow{PA}$+$\overrightarrow{PB}$|=4，可得PM=|$\overrightarrow{PM}$|=2，故点P在以点M为圆心、半径等于2的圆上，
由于OM=5，
∴动点P到坐标原点O的距离的最大值为OM+2=7．
点评 本题主要考查直线经过定点问题，直线和圆的位置关系的应用，属于中档题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
18．方程-sinx=（$\frac{1}{2}$）x在区间（0，100π）内解的个数是（ ）
| A． | 98 | B． | 100 | C． | 102 | D． | 200 |
15．
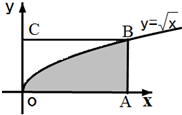如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）
如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{12}$ |
2．“光盘行动”倡导厉行节约，反对铺张浪费，带动大家珍惜粮食，吃光盘子中的食物，得到从中央到民众的支持，为了解某地响应“光盘行动”的实际情况，某校几位同学组成研究性学习小组，从某社区[25，55]岁的人群中随机抽取n人进行了一次调查，得到如下统计表：
（Ⅰ）求a，b的值，并估计本社区[25，55]岁的人群中“光盘族”所占比例；
（Ⅱ）从年龄段在[35，40）与[40，45）的“光盘族”中，采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队．
（i）已知选取2人中1人来自[35，40）中的前提下，求另一人来自年龄段[40，45）中的概率；
（ii）求2名领队的年龄之和的期望值（每个年龄段以中间值计算）．
| 组数 | 分组 | 频数 | 频率 | “光盘族”占本组比例 |
| 第1组 | [25，30） | 50 | 0.05 | 30% |
| 第2组 | [30，35） | 100 | 0.10 | 30% |
| 第3组 | [35，40） | 150 | 0.15 | 40% |
| 第4组 | [40，45） | 200 | 0.20 | 50% |
| 第5组 | [45，50） | a | b | 65% |
| 第6组 | [50，55） | 200 | 0.20 | 60% |
（Ⅱ）从年龄段在[35，40）与[40，45）的“光盘族”中，采用分层抽样方法抽取8人参加节约粮食宣传活动，并从这8人中选取2人作为领队．
（i）已知选取2人中1人来自[35，40）中的前提下，求另一人来自年龄段[40，45）中的概率；
（ii）求2名领队的年龄之和的期望值（每个年龄段以中间值计算）．