Question

3．设点A（x₀，y₀）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上的定点（x₀≠±a）…又E，F是C上的两个动点直线AE，AF的斜率互为相反数．证明：直线EF的斜率为定值．

Answer 1

分析 如图所示，设E（x₁，y₁），F（x₂，y₂）．设直线AE的斜率为k，则直线AF的斜率为-k．直线AE的方程为：y-y₀=k（x-x₀），则直线AF的方程为y-y₀=-k（x-x₀）．与椭圆的方程联立化为：（b²+a²k²）x²+2a²k（y-kx₀）x+${a}^{2}（{y}_{0}-k{x}_{0}）^{2}$-a²b²=0，△＞0，利用根与系数的关系可得：x₀+x₁，可得x₁，x₂．可得x₂-x₁，x₁+x₂-2x₀．
利用斜率计算公式可得：k_EF=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{-k（{x}_{2}+{x}_{1}-2{x}_{0}）}{{x}_{2}-{x}_{1}}$，即可证明．

解答 证明：如图所示，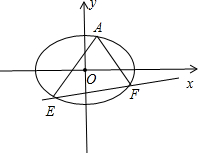
设E（x₁，y₁），F（x₂，y₂）．
设直线AE的斜率为k，则直线AF的斜率为-k．
直线AE的方程为：y-y₀=k（x-x₀），则直线AF的方程为y-y₀=-k（x-x₀）．
联立$\left\{\begin{array}{l}{y=kx+{y}_{0}-k{x}_{0}}\\{{b}^{2}{x}^{2}+{a}^{2}{y}^{2}={a}^{2}{b}^{2}}\end{array}\right.$，
化为（b²+a²k²）x²+2a²k（y-kx₀）x+${a}^{2}（{y}_{0}-k{x}_{0}）^{2}$-a²b²=0，
△＞0，
∴x₀+x₁=$\frac{2{a}^{2}k（k{x}_{0}-{y}_{0}）}{{b}^{2}+{a}^{2}{k}^{2}}$，
∴${x}_{1}=\frac{{a}^{2}{k}^{2}{x}_{0}-2{a}^{2}k{y}_{0}-{b}^{2}{x}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}$，
同理可得：x₂=$\frac{{a}^{2}{k}^{2}{x}_{0}+2{a}^{2}k{y}_{0}-{b}^{2}{x}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}$，
∴x₂-x₁=$\frac{4{a}^{2}k{y}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}$，x₁+x₂-2x₀=$\frac{-4{b}^{2}{x}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}$．
∴k_EF=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$=$\frac{-k（{x}_{2}+{x}_{1}-2{x}_{0}）}{{x}_{2}-{x}_{1}}$=$\frac{-k•\frac{-4{b}^{2}{x}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}}{\frac{4{a}^{2}k{y}_{0}}{{b}^{2}+{a}^{2}{k}^{2}}}$=$\frac{{b}^{2}}{{a}^{2}}•\frac{{x}_{0}}{{y}_{0}}$为定值．

点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、斜率计算公式，考查了推理能力与计算能力，属于难题．