如图在多面体ABC-A1B1C1中.AA1$\underset{∥}{=}$BB1.B1C1$\underset{∥}{=}$$\frac{1}{2}$BC.求证:AB1∥平面 A1C1C．题目和参考答案——青夏教育精英家教网—

题目内容

18．

如图在多面体ABC-A₁B₁C₁中，AA₁$\underset{∥}{=}$BB₁，B₁C₁$\underset{∥}{=}$$\frac{1}{2}$BC，求证：AB₁∥平面 A₁C₁C．

分析取BC的中点D，连接AD，DC₁，则四边形B₁DCC₁和BDC₁B₁为平行四边形，从而可证平面AB₁D∥平面A₁C₁C，即可得到AB₁∥平面A₁C₁C．

解答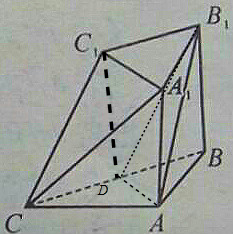证明：取BC的中点D，连接AD，DC₁，则CD平行且等于B₁C₁，BD平行且等于B₁C₁，
∴四边形B₁DCC₁和BDC₁B₁为平行四边形，
∴B₁D平行且等于CC₁，∴C₁D平行且等于B₁B，
由B₁B平行且等于AA₁，∴C₁D平行且等于A₁A，
∴四边形AA₁C₁D为平行四边形，
∴AD∥A₁C₁
∵B₁D∩AD=D，B₁D，AD?平面AB₁D，
∴平面AB₁D∥平面A₁C₁C，
∵AB₁?平面AB₁D，
∴AB₁∥平面A₁C₁C．

点评本题主要考查了直线与平面平行的判定，平面与平面平行的判定，考查了空间想象能力和推理论证能力，属于中档题．

练习册系列答案

	A．	f（1）＞e，f（2012）＞e²⁰¹²		B．	f（1）＞e，f（2012）＜e²⁰¹²
	C．	f（1）＜e，f（2012）＞e²⁰¹²		D．	f（1）＜e，f（2012）＜e²⁰¹²

9．若f（x）=x²-x+b，且f（log₂a）=b，log₂|f（a）|=2（a≠1），当满足log₂（2-x）≤2时，求f（2^x）的最小值及对应的x值．

6．已知函数f（x）=e^x-ax-1（a∈R）．
（1）求函数f（x）的单调区间；
（2）函数F（x）=f（x）-xlnx在定义域内存在零点，求a的取值范围；
（3）若g（x）=ln（e^x-1）-lnx，当x∈（0，+∞）时，不等式f（g（x））＜f（x）恒成立，求a的取值范围．

13．已知函数f（x）=lg（x+1）-ln（1-x）的定义域为A，g（x）=$\sqrt{2x-1}$的定义域为B，则A∩B=（　　）

3．设点A（x₀，y₀）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上的定点（x₀≠±a）…又E，F是C上的两个动点直线AE，AF的斜率互为相反数．证明：直线EF的斜率为定值．

10．定义在R上的函数f（x）在[8，+∞）上为减函数，且函数y=f（x+8）为奇函数，则f（x）的图象关于（8，0）对称，且f（x）在（-∞，8）上为减函数（填增、减）．

7．函数y=lg（12+x-x²）的单调递增区间是（-3，$\frac{1}{2}$]．

8．在△ABC中，∠B=45°，AC=$\sqrt{5}$，cosC=$\frac{{3\sqrt{10}}}{10}$，求
（1）BC的长
（2）若点D是AB的中点，求中线CD的长度．

试题分类