题目内容
已知点O(0,0),A(-1,1),若F为双曲线x2-y2=1的右焦点,P是该双曲线上且在第一象限的动点,则
•
的取值范围为( )
| OA |
| FP |
A、(
| ||||
B、(
| ||||
C、(1,
| ||||
D、(
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:用坐标表示出
•
,利用直线过(1,0)时,t=
-1,直线为渐近线y=x时,t=
,即可得出结论.
| OA |
| FP |
| 2 |
| 2 |
解答:
解:设P(x,y),则
∵F(
,0),
∴
•
=(-1,1)•(x-
,y)=-x+y+
,
令t=-x+y+
,则y=x+t-
是与渐近线平行的直线,
直线过(1,0)时,t=
-1,直线为渐近线y=x时,t=
,
∵P是该双曲线上且在第一象限的动点,
∴
-1<t<
.
故选:B.
∵F(
| 2 |
∴
| OA |
| FP |
| 2 |
| 2 |
令t=-x+y+
| 2 |
| 2 |
直线过(1,0)时,t=
| 2 |
| 2 |
∵P是该双曲线上且在第一象限的动点,
∴
| 2 |
| 2 |
故选:B.
点评:本题考查双曲线的简单性质,考查向量的数量积公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
在数列{an}中,如果a1=1,且an+1=
an,则a3等于( )
| 1 |
| 2 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
已知集合A={x|y=
},B={y|y=2x,x>0},则A∪B=( )
| 9-x2 |
| A、{x|x>1} |
| B、{x|1<x≤3} |
| C、{x|x≥-3} |
| D、∅ |
已知角α的终边经过点p(2,2),tanα=( )
| A、1 | ||||
B、
| ||||
| C、-1 | ||||
D、-
|
已知集合A={x|x=
+
π,k∈Z},B={x|x=
+
π,k∈Z},则( )
| kπ |
| 2 |
| 1 |
| 4 |
| kπ |
| 4 |
| 1 |
| 2 |
| A、A=B | B、A?B |
| C、A?B | D、A∩B=∅ |
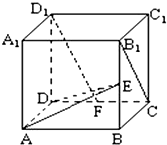 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.