题目内容
10.sin17°sin223°+sin253°sin313°=( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 先利用诱导公式把原式的各项化简后,然后利用两角和的正弦函数公式及特殊角的三角函数值即可求出原式的值.
解答 解:sin17°•sin223°+sin253°•sin313°
=sin17°•sin(270°-47°)+sin(270°-17°)•sin(360°-47°)
=sin17°(-cos47°)+(-cos17°)(-sin47°)
=sin47°cos17°-cos47°sin17°
=sin(47°-17°)
=sin30°
=$\frac{1}{2}$.
故选:B.
点评 此题考查学生灵活运用诱导公式及两角和与差的正弦函数公式化简求值,学生做题时应注意角度的灵活变换,属于基础题.

练习册系列答案
相关题目
19.下列说法错误的是( )
| A. | 在统计学中,独立性检验是检验两个分类变量是否有关系的一种统计方法 | |
| B. | 在残差图中,残差分布的带状区域的宽度越狭窄,其模拟的效果越好 | |
| C. | 线性回归方程对应的直线$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$至少经过其样本数据点中的一个点 | |
| D. | 在回归分析中,相关指数R2越大,模拟的效果越好 |
20.若集合P={-2,0,2},i是虚数单位,则( )
| A. | 2i∈P | B. | $\frac{2}{i}$∈P | C. | ($\sqrt{2}$i)2∈P | D. | $\frac{2}{{i}^{3}}$∈P |
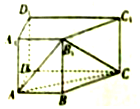 如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.
如图,在直四棱柱ABCD-A1B1C1D1中,AB∥DC,AA1=1,AB:AD:BC:DC=3:4:5:6,侧棱AA1⊥底面ABCD.