题目内容
斜率为1的直线过抛物线y2=4x的焦点,与抛物线相交于A,B两点(A点在x轴上方).
(1)求A点坐标.
(2)求线段AB的长.
(1)求A点坐标.
(2)求线段AB的长.
分析:(1)根据抛物线的方程算出抛物线的焦点为F(1,0),从而得到题中的直线方程为y=x-1,将直线方程与抛物线方程联解,得到方程组的解并结合A点在x轴的上方加以判别,即可得到A点坐标.
(2)设A、B两点的坐标分别为(xA,yA)、(xB,yB),根据(1)中得到的一元二次方程,利用根与系数的关系可得xA+xB=6,由此结合抛物线的定义加以运算,可得线段AB的长.
(2)设A、B两点的坐标分别为(xA,yA)、(xB,yB),根据(1)中得到的一元二次方程,利用根与系数的关系可得xA+xB=6,由此结合抛物线的定义加以运算,可得线段AB的长.
解答:解:(1)设A、B两点的坐标分别为(xA,yA)、(xB,yB),
∵抛物线y2=4x中,2p=4,得
=1,
∴抛物线的焦点为F(1,0),
由此可得经过焦点且斜率为1的直线方程为y=x-1,
根据
,消去y,
得x2-6x+1=0,
解得x=
=3±2
.
∵直线与抛物线相交于A、B两点,且A点在x轴上方,
∴A点的横坐标大于1,可得xA=3+2
,
代入直线方程可得yA=2+2
.
因此,点A的坐标为(3+2
,2+2
);
(2)由(1)可得xA、xB是方程x2-6x+1=0的两个实数根,
∴xA+xB=6,xAxB=1,
又∵点A、B在抛物线上,∴根据抛物线的定义,
得|AF|=xA+
=xA+1,|BF|=xB+
=xB+1.
因此,|AB|=|AF|+|BF|=(xA+1)+(xB+1)=(xA+xB)+2=8,
即线段AB的长等于8.
∵抛物线y2=4x中,2p=4,得
| p |
| 2 |
∴抛物线的焦点为F(1,0),
由此可得经过焦点且斜率为1的直线方程为y=x-1,
根据
|
得x2-6x+1=0,
解得x=
6±
| ||
| 2 |
| 2 |
∵直线与抛物线相交于A、B两点,且A点在x轴上方,
∴A点的横坐标大于1,可得xA=3+2
| 2 |
代入直线方程可得yA=2+2
| 2 |
因此,点A的坐标为(3+2
| 2 |
| 2 |
(2)由(1)可得xA、xB是方程x2-6x+1=0的两个实数根,
∴xA+xB=6,xAxB=1,
又∵点A、B在抛物线上,∴根据抛物线的定义,
得|AF|=xA+
| p |
| 2 |
| p |
| 2 |
因此,|AB|=|AF|+|BF|=(xA+1)+(xB+1)=(xA+xB)+2=8,
即线段AB的长等于8.
点评:本题给出抛物线的焦点弦的斜率为1,求焦点弦的长度.着重考查了抛物线定义与标准方程、直线与圆锥曲线的位置关系等知识,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
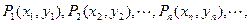 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数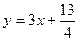 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以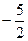 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.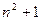 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求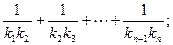
 设
设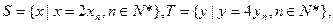 等差数列
等差数列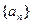 的任一项
的任一项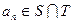 ,其中
,其中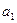 是
是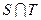 中的最大数,
中的最大数,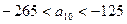 ,求数列
,求数列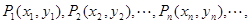 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数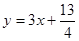 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以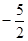 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}. ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求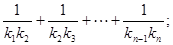
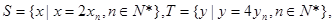 等差数列
等差数列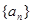 的任一项
的任一项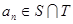 ,其中
,其中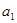 是
是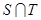 中的最大数,
中的最大数,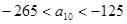 ,求数列
,求数列